下载APP
【简答题】
从一个总体中随机抽取n=100的随机样本，得到
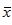=104560，假定总体标准差σ=85414，构建总体均值μ的95%的置信区间。
参考答案：
参考解析：
刷刷题刷刷变学霸
举一反三
【单选题】某无限总体的总体成数是0.2。从中抽取100个体作为随机样本，则样本成数的均值和标准差是（）
A.
0.2和0.04
B.
0.2和0.2
C.
20和0.04
D.
20和0.2
【单选题】从正态总体中随机抽取一个n=10的随机样本，计算得到=231.7，s2=15.5，假定=50，在α=0.05的显著性水平下，检验假设，得到的结论是（）。
A.
拒绝H0
B.
不拒绝H0
C.
可以拒绝也可以不拒绝H0
D.
可能拒绝也可能不拒绝H0
【单选题】从正态总体中抽取一个n=20的随机样本,得到样本标准差s=5,总体标准差95%的置信区间为
A.
[1.8,5.3]
B.
[2.8,6.3]
C.
[3.8,7.3]
D.
[4.8,8.3]
【单选题】设容量为16人的简单随机样本,平均完成工作时间13分钟,总体服从正态分布且标准差为3分钟。 若想对完成工作所需时间构造一个90%置信区间,则
A.
应用标准正态概率表查出z值
B.
应用t-分布表查出t值
C.
应用二项分布表查出p值
D.
应用泊松分布表查出λ值
【单选题】抽自两个总体的独立随机样本提供的信息如下表: 在α=0.05的显著性水平下,检验假设H 0 :μ 1 -μ 2 =0,H 1 :μ 1 -μ 2 ≠0,得到的结论是( )。
A.
拒绝H 0
B.
不拒绝H 0
C.
可以拒绝也可以不拒绝H 0
D.
可能拒绝也可能不拒绝H 0
【单选题】正态总体方差未知,小样本条件下,总体均值 的 双侧置信区间的长度()
A.
会随样本容量的增大而变短
B.
不会随样本容量的增大而变短
C.
会随样本容量的增大而变长
D.
不会随样本容量的增大而变长
【单选题】随机地从一批零件中抽取16个，测得其长度(单位：cm)如下： 2.14，2.10，2.13，2.15，2.13，3.12，2.13，2.10 2.15，2.10，2.14，2.10，2.13，2.11，2.14，2.11 该零件长度分布为正态的且σ=0.01(cm)，则总体均值μ的置信度为0.95的置信区间是 ( )。
A.
[2.1，2.2]
B.
[2.1201，2.1299]
C.
[2.13，2.14]
D.
[2.2，2.31]
【单选题】为估计学生的平均年龄,随机抽出一个 n=60 的样本,算得 =25.3岁,总体方差是 =16,总体均值 的95%的置信区间为 ( )。
A.
（22.29,24.31)
B.
(23.29,25.31)
C.
(24.29,26.31)
D.
(25.29,27.31)
【单选题】设容量为16人的简单随机样本，平均完成工作需时13分钟。已知总体标准差为3分钟。若想对完成工作所需时间总体构造一个90%置信区间，则（）
A.
应用标准正态概率表查出u值
B.
应用t分布表查出t值
C.
应用卡方分布表查出卡方值
D.
应用F分布表查出F值
相关题目：
【多选题】设总体X~N(9,9),【图片】是来自X的简单随机样本，【图片】是样本均值，以下结果正确的是
A.
B.
与 相互独立
C.
D.
E.
与 不独立
F.
【单选题】某无限总体的总体成数是0.2。从中抽取100个体作为随机样本，则样本成数的均值和标准差是（）
A.
0.2和0.04
B.
0.2和0.2
C.
20和0.04
D.
20和0.2
【单选题】从正态总体中随机抽取一个n=10的随机样本，计算得到=231.7，s2=15.5，假定=50，在α=0.05的显著性水平下，检验假设，得到的结论是（）。
A.
拒绝H0
B.
不拒绝H0
C.
可以拒绝也可以不拒绝H0
D.
可能拒绝也可能不拒绝H0
【单选题】对同一人群的两个随机样本进行调查，其结果的一致程度被称为
A.
真实性
B.
可靠性
C.
灵敏度
D.
特异度
E.
约登指数
【单选题】设 是来自 的简单随机样本,则 , =( ).
A.
;
B.
;
C.
;
D.
.
【单选题】从正态总体中抽取一个n=20的随机样本,得到样本标准差s=5,总体标准差95%的置信区间为
A.
[1.8,5.3]
B.
[2.8,6.3]
C.
[3.8,7.3]
D.
[4.8,8.3]
【单选题】设容量为16人的简单随机样本,平均完成工作时间13分钟,总体服从正态分布且标准差为3分钟。 若想对完成工作所需时间构造一个90%置信区间,则
A.
应用标准正态概率表查出z值
B.
应用t-分布表查出t值
C.
应用二项分布表查出p值
D.
应用泊松分布表查出λ值
【单选题】抽自两个总体的独立随机样本提供的信息如下表: 在α=0.05的显著性水平下,检验假设H 0 :μ 1 -μ 2 =0,H 1 :μ 1 -μ 2 ≠0,得到的结论是( )。
A.
拒绝H 0
B.
不拒绝H 0
C.
可以拒绝也可以不拒绝H 0
D.
可能拒绝也可能不拒绝H 0
【单选题】正态总体方差未知,小样本条件下,总体均值 的 双侧置信区间的长度()
A.
会随样本容量的增大而变短
B.
不会随样本容量的增大而变短
C.
会随样本容量的增大而变长
D.
不会随样本容量的增大而变长
【单选题】随机地从一批零件中抽取16个，测得其长度(单位：cm)如下： 2.14，2.10，2.13，2.15，2.13，3.12，2.13，2.10 2.15，2.10，2.14，2.10，2.13，2.11，2.14，2.11 该零件长度分布为正态的且σ=0.01(cm)，则总体均值μ的置信度为0.95的置信区间是 ( )。
A.
[2.1，2.2]
B.
[2.1201，2.1299]
C.
[2.13，2.14]
D.
[2.2，2.31]
【单选题】为估计学生的平均年龄,随机抽出一个 n=60 的样本,算得 =25.3岁,总体方差是 =16,总体均值 的95%的置信区间为 ( )。
A.
（22.29,24.31)
B.
(23.29,25.31)
C.
(24.29,26.31)
D.
(25.29,27.31)
【单选题】设容量为16人的简单随机样本，平均完成工作需时13分钟。已知总体标准差为3分钟。若想对完成工作所需时间总体构造一个90%置信区间，则（）
A.
应用标准正态概率表查出u值
B.
应用t分布表查出t值
C.
应用卡方分布表查出卡方值
D.
应用F分布表查出F值