
下载APP

【简答题】


计算三重积分,其中Ω是由锥面与柱面x2+y2=1以及z=0围成的空间区域(见图8.6).
利用柱面坐标计算三重积分I=
∭Ω(x2+y2)dV,其与柱面x2+y2=1以及z=0围成的空间区域。参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】设空间区域$\Omega =\left\{ (x,y,z)|\sqrt{{{x}^{2}}+{{y}^{2}}}\le z\le 1 \right\}$,则三重积分$\iiint\limits {\Omega }{\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}x\text{d}y\text{d}z}=$ ( ).
A.
$\text{ }\!\!\pi\!\!\text{ }$
B.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$
C.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$
D.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
相关题目:

【多选题】下列空间闭区域中,能使三重积分的值为0的是( ).
A.


B.
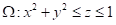
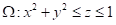
C.


D.
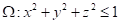
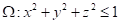
【单选题】设空间区域$\Omega =\left\{ (x,y,z)|\sqrt{{{x}^{2}}+{{y}^{2}}}\le z\le 1 \right\}$,则三重积分$\iiint\limits {\Omega }{\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}x\text{d}y\text{d}z}=$ ( ).
A.
$\text{ }\!\!\pi\!\!\text{ }$
B.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$
C.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$
D.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$
【单选题】设积分区域G是由坐标面和平面x+2y+3z=6所围成的,则三重积分 ( )
A.
6
B.
12
C.
18
D.
36
【判断题】在柱面坐标下的体积元:dV=rdrdzdθ
A.
正确
B.
错误
【单选题】设为立方体:,则三重积分=( )
A.
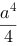
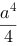
B.
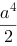
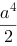
C.


D.
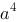
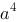
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
【单选题】设是由球面所围成的闭区域,则三重积分( )。
A.
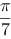
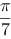
B.
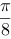
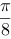
C.


D.
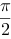
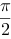
【单选题】设有两空间区域,,则以下结论正确的是( )
A.


B.


C.


D.



