下载APP

【判断题】


设f(x)=1/(1+e^-x),则该函数的导数为f'(x)=f(x)/(1-f(x)),f'(x)始终大于0,因此f(x)在整个定义域上为单调递增函数。
A.
正确
B.
错误
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】(理)已知函数 的定义域为R,当 时, ,且对任意的实数 , ,等式 恒成立.若数列{ }满足 ,且 = ,则 的值为
A.
4018
B.
4019
C.
4020
D.
4021
【简答题】已知奇函数f(x)是定义在(-1,1)上的增函数,若f(m-1)+f(2m-1)≤0,则m的取值范围是( )
A.
(-∞, 2 3 )
B.
(-∞, 2 3 ]
C.
(0, 2 3 )
D.
(0, 2 3 ]
【简答题】f(x),g(x)都是定义在R上的单调递增函数,f(x)>0,g(x)<0,则 f(x) g(x) ( )
A.
大于0,单调递增
B.
小于0,单调递减
C.
小于0,单调递增
D.
小于0,单调性无法确定
【单选题】若偶函数f(x)在(-∞,-1]上是增函数,则( )
A.
f(-1.5)<f(-1)<f(2)
B.
f(-1)<f(-1.5)<f(2)
C.
f(2)<f(-1)<f(-1.5)
D.
f(2)<f(-1.5)<f(-1)
【单选题】$f(x,y)=\sqrt{1-x^2}+\sqrt{y^2-1}$的定义域为
A.
$\{(x,y)\mid|x|+|y|\lt 1\}$
B.
$\{(x,y)\mid |x|\lt 1,|y|\gt 1\}$
C.
$\{(x,y)\mid x^2+y^2\gt 1\}$
D.
$\{(x,y)\mid |x|\leqslant 1,|y|\geqslant 1\}$
相关题目:

【判断题】在给定的定义域范围内,函数一阶导数大于0,则函数在此区间内是增函数。
A.
正确
B.
错误
【单选题】(理)已知函数 的定义域为R,当 时, ,且对任意的实数 , ,等式 恒成立.若数列{ }满足 ,且 = ,则 的值为
A.
4018
B.
4019
C.
4020
D.
4021
【单选题】下列四个函数中,在(0,1)上为增函数的是
A.
y=sinx
B.
y=-log2x
C.
y=( )x
)x
 )x
)xD.
y=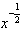
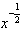
【简答题】已知奇函数f(x)是定义在(-1,1)上的增函数,若f(m-1)+f(2m-1)≤0,则m的取值范围是( )
A.
(-∞, 2 3 )
B.
(-∞, 2 3 ]
C.
(0, 2 3 )
D.
(0, 2 3 ]
【简答题】f(x),g(x)都是定义在R上的单调递增函数,f(x)>0,g(x)<0,则 f(x) g(x) ( )
A.
大于0,单调递增
B.
小于0,单调递减
C.
小于0,单调递增
D.
小于0,单调性无法确定
【单选题】若偶函数f(x)在(-∞,-1]上是增函数,则( )
A.
f(-1.5)<f(-1)<f(2)
B.
f(-1)<f(-1.5)<f(2)
C.
f(2)<f(-1)<f(-1.5)
D.
f(2)<f(-1.5)<f(-1)
【单选题】下列函数是偶函数且在 上是增函数的是
A.
B.
C.
【单选题】$f(x,y)=\sqrt{1-x^2}+\sqrt{y^2-1}$的定义域为
A.
$\{(x,y)\mid|x|+|y|\lt 1\}$
B.
$\{(x,y)\mid |x|\lt 1,|y|\gt 1\}$
C.
$\{(x,y)\mid x^2+y^2\gt 1\}$
D.
$\{(x,y)\mid |x|\leqslant 1,|y|\geqslant 1\}$