
下载APP

【单选题】


设A是秩为n-1的n阶矩阵,α1与α2是方程组Ax=0的两个不同的解向量,则Ax=0的通解必定是( )。
A.
α1+α2
B.
kα1
C.
k(α1+α2)
D.
k(α1-α2)
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】若A,B都是n阶矩阵,则下面结论正确的是( )
A.
若A与B合同,则A与B有相同的秩
B.
若A与B合同,则A与B的行列式相等
C.
若A与B有相同的秩,则A与B合同
D.
以上都正确
【多选题】设是阶矩阵,是的特征值,是的分别对应于的特征向量,则下列说法错误的是( ).
A.
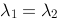 时,
时,
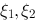 一定不成比例
一定不成比例
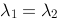 时,
时,
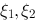 一定不成比例
一定不成比例B.
 时,
时,
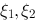 一定不成比例
一定不成比例
 时,
时,
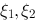 一定不成比例
一定不成比例C.
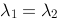 时,
时,
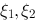 一定成比例
一定成比例
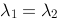 时,
时,
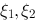 一定成比例
一定成比例D.
 时,
时,
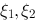 一定成比例
一定成比例
 时,
时,
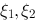 一定成比例
一定成比例【单选题】设A是秩为n-1的n阶矩阵,α1与α2是方程组Ax=0的两个不同的解向量,则Ax=0的通解必定是( )。
A.
α1+α2
B.
kα1
C.
k(α1+α2)
D.
k(α1-α2)
【单选题】设方程组\[\left\{ {\begin{array}{*{20}{c}} {\lambda {x_1} + {x_2} + {x_3} = \lambda - 3}\\ {{x_1} + \lambda {x_2} + {x_3} = - 2}\\ {{x_1} + {x_2} + \lambda {x_3} = - 2} \end{array}} \right.\]若`\lambda \ne...
A.
无解
B.
有唯一解
C.
有非零解
D.
有无穷多解
【单选题】设n阶矩阵A与B相似,E为n阶单位矩阵,则( )
A.
λE-A=λE-B
B.
A与B有相同的特征值和特征向量.
C.
A和B都相似于一个对角矩阵.
D.
对任意常数t,tE-A与tE-B相似.
相关题目:

【判断题】任何阶矩阵的盖尔圆都可以通过相似变换隔离成个孤立的盖尔圆。( )
A.
正确
B.
错误
【单选题】若A,B都是n阶矩阵,则下面结论正确的是( )
A.
若A与B合同,则A与B有相同的秩
B.
若A与B合同,则A与B的行列式相等
C.
若A与B有相同的秩,则A与B合同
D.
以上都正确
【多选题】设是阶矩阵,是的特征值,是的分别对应于的特征向量,则下列说法错误的是( ).
A.
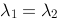 时,
时,
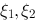 一定不成比例
一定不成比例
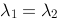 时,
时,
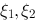 一定不成比例
一定不成比例B.
 时,
时,
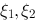 一定不成比例
一定不成比例
 时,
时,
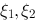 一定不成比例
一定不成比例C.
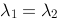 时,
时,
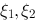 一定成比例
一定成比例
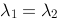 时,
时,
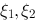 一定成比例
一定成比例D.
 时,
时,
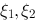 一定成比例
一定成比例
 时,
时,
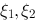 一定成比例
一定成比例【单选题】设矩阵,且3阶矩阵B满足ABC=D,则|B-1|=()
A.
﹣1/6
B.
1/6
C.
﹣1/3
D.
1/3
【单选题】设A是秩为n-1的n阶矩阵,α1与α2是方程组Ax=0的两个不同的解向量,则Ax=0的通解必定是( )。
A.
α1+α2
B.
kα1
C.
k(α1+α2)
D.
k(α1-α2)
【单选题】设n阶矩阵A与B相似,E为n阶单位矩阵,则( )
A.
λE-A=λE-B
B.
A与B有相同的特征值和特征向量.
C.
A和B都相似于一个对角矩阵.
D.
对任意常数t,tE-A与tE-B相似.
【单选题】设三阶矩阵A的特征值为-1,3,4,则A的伴随矩阵的特征值为
A.
12,-4,-3
B.
-1,1/3,1/4
C.
2,5,6
D.
-1,6,9
【单选题】若3阶矩阵A的行列式|A|=0,则()。
A.
A有一行为0
B.
A有一行是其余行的线性组合
C.
A=0
D.
A的两行成比例
【单选题】设【图片】是【图片】矩阵,【图片】,【图片】是【图片】的伴随矩阵,则【图片】的基础解系中解向量的个数为( ).
A.
4
B.
3
C.
1
D.
无法确定

