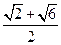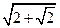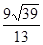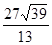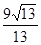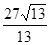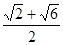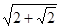下载APP

参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
【单选题】类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列性质,你认为比较恰当的是 ①各棱长相等,同一顶点上的任两条棱的夹角相等;②各个面是全等的正三角形,相邻的两个面所成的二面角相等;③各个面都是全等的正三角形,同一顶点的任两条棱的夹角相等;④各棱长相等,相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③
相关题目:

【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
【单选题】如图,在直角三角形中(∠=90o),放置边长分别3,4,的三个正方形,则的值为
A.
5
B.
6
C.
7
D.
12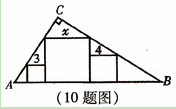

【单选题】如图,四边形ABCD是菱形,四边形ACEF是正方形,若AC=2,∠B=60°,则图中阴影部分的面积是 [ ]
A.
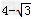
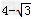
B.
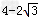
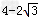
C.
3
D.
2
【单选题】在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是 ( )
A.
4条
B.
6条
C.
8条
D.
10条
【单选题】如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )
A.
B.
16
C.
8
D.
4
【判断题】焦距长度大于像平面对角线的镜头,称为长焦距镜头
A.
正确
B.
错误

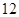 ,底面对角线的长为
,底面对角线的长为
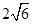 ,则侧面与底面所成的二面角等于
,则侧面与底面所成的二面角等于