
下载APP

点到直线、平面的距离题库

题数
2000
考试分类
高中数学>点到直线、平面的距离
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-点到直线、平面的距离
...更多
题目预览
【简答题】

[1/2000]如图,在三棱柱 【图片】中,侧棱 【图片】底面 【图片】, 【图片】为 【图片】的中点, 【图片】, 【图片】. 【图片】(1)求证: 【图片】平面 ...
参考答案:
|
(1)见解析;(2)
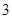 . .
|
参考解析:
(1)欲证
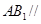 平面
平面
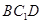 ,根据线面平行的判定定理可知只需证
,根据线面平行的判定定理可知只需证
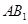 与平面
与平面
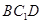 内一直线平行,连接
内一直线平行,连接
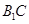 ,设
,设
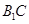 与
与
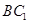 相交于点O,连接
相交于点O,连接
 ,根据中位线定理可知
,根据中位线定理可知
 ∥
∥
 ,
,
 ⊂平面
⊂平面
 ,
,
 ⊄平面
⊄平面
 ,满足定理所需条件;
,满足定理所需条件;
(2)根据面面垂直的判定定理可知平面
 ⊥平面
⊥平面
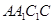 ,作
,作
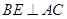 ,垂足为E,则
,垂足为E,则
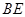 ⊥平面
⊥平面
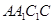 ,然后求出棱长,最后根据四棱锥
,然后求出棱长,最后根据四棱锥
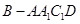 ,的体积
,的体积
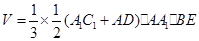 ,即可求四棱锥
,即可求四棱锥
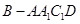 的体积.
的体积.
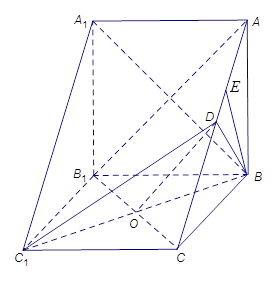
(1)证明:连接
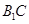 ,设
,设
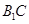 与
与
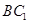 相交于点
相交于点
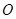 ,连接
,连接
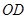 ,
,
∵ 四边形
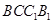 是平行四边形,
是平行四边形,
∴点
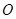 为
为
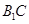 的中点.
的中点.
∵
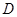 为
为
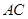 的中点,
的中点,
∴
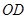 为△
为△
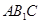 的中位线,
的中位线,
∴
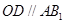 .
.
∵
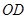
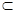 平面
平面
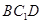 ,
,
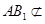 平面
平面
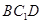 ,
,
∴
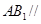 平面
平面
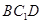 .
.
(2)∵
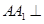 平面
平面
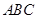 ,
,
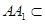 平面
平面
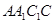 ,
,
∴ 平面
 平面
平面
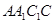 ,且平面
,且平面
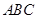
 平面
平面
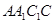
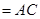 .
.
作
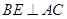 ,垂足为
,垂足为
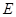 ,则
,则
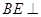 平面
平面
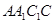 ,
,
∵
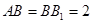 ,
,
 ,
,
在Rt△
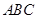 中,
中,
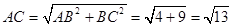 ,
,
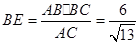 ,
,
∴四棱锥
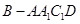 的体积
的体积
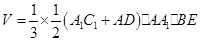
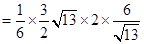
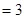 .
.
∴四棱锥
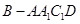 的体积为
的体积为
 .
.
【简答题】

[2/2000]在正方体 【图片】中,下列几种说法错误的是 A. 【图片】B. 【图片】C. 【图片】与 【图片】成 【图片】角D. 【图片】与 【图片】成 【图片】...
参考答案:
|
B
|
参考解析:
如图,
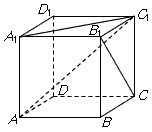
A选项中
 在平面
在平面
 上的投影为
上的投影为
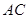 ,而
,而
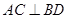 ,故
,故
 ,A正确
,A正确
B选项中,
 ,故
,故
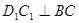 ,B正确
,B正确
C选项中,
【简答题】

[3/2000]如图,矩形 【图片】中, 【图片】, 【图片】, 【图片】为 【图片】上的点,且 【图片】,AC、BD交于点G. 【图片】(1)求证: 【图片】; (...
参考答案:
|
(1)利用线线垂直证明线面垂直;(2)利用线线平行证明线面平行;(3)
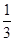 . .
|
参考解析:
(1)证明:
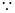
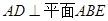 ,
,
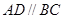
∴
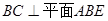 ,
,
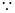 AE
AE
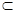 平面ABE, ∴
平面ABE, ∴
 2分
2分
又
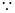
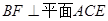 ,∴
,∴
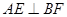 3分
3分
又∵BC∩BF=B,
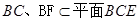 ,
,
∴
 ..4分
..4分
(2)证明:依题意可知:
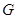 是
是
 中点.
中点.
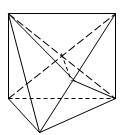
由
 知
知
 ,而
,而
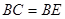 ,
,
∴
 是
是
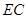 中点,
中点,
∴ 在
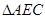 中,
中,
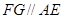 , 6分
, 6分
又∵FG
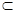 平面BFD,AE
平面BFD,AE
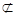 平面BFD,
平面BFD,
∴
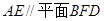 8分
8分
(3)解:
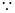
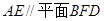 , ∴
, ∴
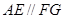 ,而
,而
 ,
,
∴
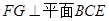 ,即
,即
 .9分
.9分
 是
是
 中点,
中点,
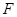 是
是
 中点, ∴
中点, ∴
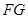
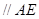 且
且
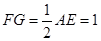 .
.
又知在
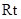 △
△
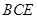 中,
中,
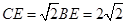 ,
,
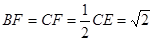 ,
,
∴
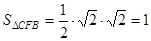 11分
11分
∴
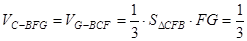 . .12分
. .12分
点评:在求几何体的体积时,当所给的几何体为“规则”的柱体、椎体或台体时,直接利用公式求解.当所给几何体的体积不能直接运用公式求解时,常利用转换法、分割法、补形法等方法
【简答题】

[4/2000]如图,AB是圆O的直径,CA垂直圆O所在的平面,D是圆周上一点,已知AC= 【图片】。AD= 【图片】。 (Ⅰ)求证:平面ADC⊥平面CDB;(Ⅱ)求...
参考答案:
|
(Ⅰ)∵CA⊥平面ADB ∴CA⊥BD,又D是圆周上一点,故BD⊥AD∴BD⊥平面ACD ∵BD
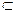 平面BCD ∴平面CDB⊥平面CAD 平面BCD ∴平面CDB⊥平面CAD
(Ⅱ)又(Ⅰ)知BD⊥平面ADC, ∴BD⊥AD,BD⊥CD,故∠CDA就是二面角C—DB—A的平面角。又 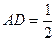 , ,
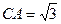 , ,
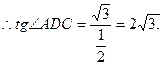 ∴平面ADB与平面ADC所成二面角的平面角的正切值为 ∴平面ADB与平面ADC所成二面角的平面角的正切值为
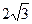 。 。
|
参考解析:
无
【简答题】

[5/2000]如图,在矩形 【图片】中,点 【图片】为边 【图片】上的点,点 【图片】为边 【图片】的中点, 【图片】,现将 【图片】沿 【图片】边折至 【图片】位...
参考答案:
|
(1)详见解析;(2)
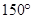 . .
|
参考解析:
(1) 利用直角三角形,先证明折前有
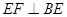 ,折后这个垂直关系没有改变,然后由平面
,折后这个垂直关系没有改变,然后由平面
 平面
平面
 的性质证明
的性质证明
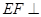 平面
平面
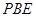 ,最后由面面垂直的判定定理即可证明平面
,最后由面面垂直的判定定理即可证明平面
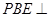 平面
平面
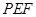 ;(2)为方便计算,不妨设
;(2)为方便计算,不妨设
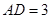 ,先以
,先以
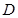 为原点,以
为原点,以
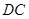 方向为
方向为
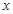 轴,以
轴,以
 方向为
方向为
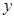 轴,以与平面
轴,以与平面
 向上的法向量同方向为
向上的法向量同方向为
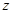 轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面
轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面
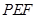 和平面
和平面
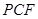 的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
(1) 证明:由题可知:折前
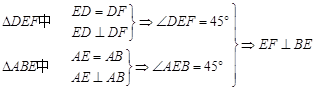 ,这个垂直关系,折后没有改变
,这个垂直关系,折后没有改变
故折后有
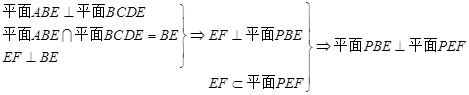
(2)不妨设
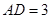 ,以
,以
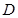 为原点,以
为原点,以
 方向为
方向为
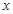 轴,以
轴,以
 方向为
方向为
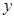 轴,以与平面
轴,以与平面
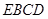 向上的法向量同方向为
向上的法向量同方向为
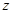 轴,建立空间直角坐标系 7分
轴,建立空间直角坐标系 7分
则
设平面
 和平面
和平面
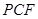 的法向量分别为
的法向量分别为
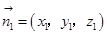 ,
,
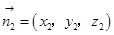
由
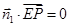 及
及
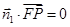 可得到
可得到
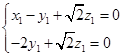 即
即
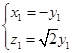 ,不妨取
,不妨取
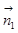
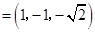
又由
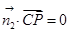 及
及
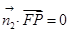 可得到
可得到
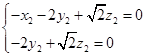 即
即
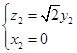
不妨取
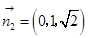 9分
9分
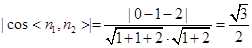 11分
11分
综上所述,二面角
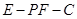 大小为
大小为
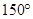 12分.
12分.
【简答题】

[6/2000]已知两条不同直线 【图片】和 【图片】及平面 【图片】,则直线 【图片】的一个充分条件是 ( ...
参考答案:
|
B
|
参考解析:
无
【简答题】

[7/2000](本题满分12分 )如图,在等腰直角 【图片】中, 【图片】, 【图片】, 【图片】, 【图片】为垂足.沿 【图片】将 【图片】对折,连结 【图片】、...
参考答案:
|
(1)在线段
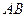 上存在点 上存在点
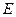 ,使 ,使
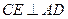 ; (2) ; (2)
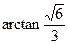
|
参考解析:
解:(1)在线段
 上存在点
上存在点
 ,使
,使
 .
.

由等腰直角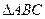 可知,对折后,
可知,对折后,
 ,
,
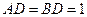 .
.
在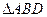 中,
中,
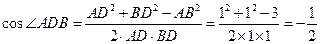 ,
,
∴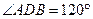 ,
,
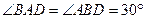 .
.
过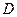 作
作
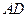 的垂线,与
的垂线,与
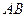 的交于点
的交于点
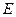 ,点
,点
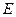 就是
就是
满足条件的唯一点.理由如下:
连结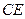 ,∵
,∵
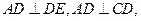
 ,∴
,∴
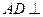 平面
平面
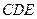 ,
,
∴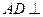
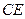 ,即在线段
,即在线段
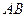 上存在点
上存在点
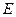 ,使
,使
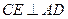 . ………………4分
. ………………4分
在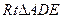 中,
中,
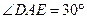 ,
,
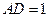 ,得
,得
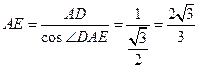 .……6分
.……6分
(2)对折后,作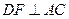 于
于
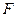 ,连结
,连结
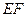 ,
,
∵ ,
,
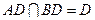 ,
,
∴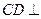 平面
平面
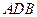 ,
,
∴平面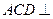 平面
平面
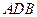 .
.
∵ ,且平面
,且平面
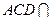 平面
平面
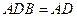 ,
,
∴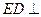 平面
平面
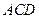 .
.
而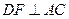 ,所以
,所以
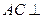 平面
平面
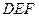 ,
,
即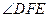 为二面角
为二面角
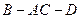 的平面角. ……………………9分
的平面角. ……………………9分
在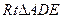 中,
中,
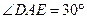 ,
,
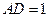 ,
,
得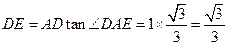 ,
,
在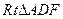 中,
中,
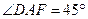 ,
,
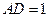 ,得
,得
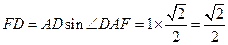 .
.
在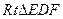 中,
中,
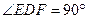 ,
,
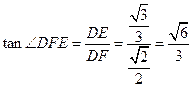 ,
,
所以二面角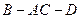 的大小为
的大小为
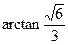 . ……………………12分
. ……………………12分
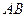 上存在点
上存在点
 ,使
,使
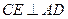 .
.

由等腰直角
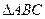 可知,对折后,
可知,对折后,
 ,
,
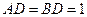 .
.
在
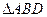 中,
中,
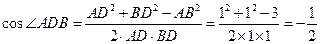 ,
,
∴
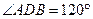 ,
,
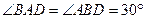 .
.
过
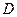 作
作
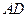 的垂线,与
的垂线,与
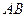 的交于点
的交于点
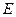 ,点
,点
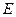 就是
就是
满足条件的唯一点.理由如下:
连结
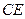 ,∵
,∵
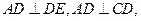
 ,∴
,∴
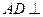 平面
平面
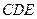 ,
,
∴
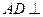
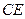 ,即在线段
,即在线段
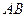 上存在点
上存在点
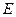 ,使
,使
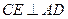 . ………………4分
. ………………4分
在
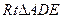 中,
中,
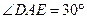 ,
,
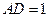 ,得
,得
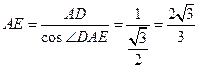 .……6分
.……6分
(2)对折后,作
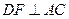 于
于
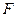 ,连结
,连结
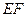 ,
,
∵
 ,
,
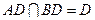 ,
,
∴
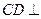 平面
平面
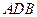 ,
,
∴平面
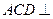 平面
平面
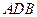 .
.
∵
 ,且平面
,且平面
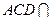 平面
平面
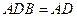 ,
,
∴
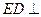 平面
平面
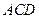 .
.
而
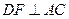 ,所以
,所以
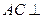 平面
平面
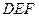 ,
,
即
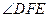 为二面角
为二面角
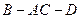 的平面角. ……………………9分
的平面角. ……………………9分
在
 中,
中,
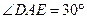 ,
,
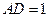 ,
,
得
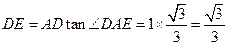 ,
,
在
 中,
中,
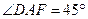 ,
,
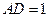 ,得
,得
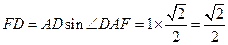 .
.
在
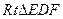 中,
中,
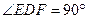 ,
,
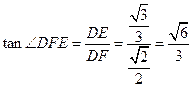 ,
,
所以二面角
 的大小为
的大小为
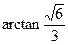 . ……………………12分
. ……………………12分
【简答题】

[8/2000](本小题满分12分) 如图:在三棱锥D-ABC中,已知 【图片】是正三角形,AB 【图片】平面BCD, 【图片】,E为BC的中点,F在棱AC上,且 【...
参考答案:
|
(1)
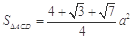 (2)先证
EF⊥
AC,再证DE⊥AC
,即可证
AC⊥平面
DEF (2)先证
EF⊥
AC,再证DE⊥AC
,即可证
AC⊥平面
DEF
(3)存在这样的点 N,当 CN= 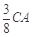 时,
MN∥平面
DEF. 时,
MN∥平面
DEF.
|
参考解析:
(1)∵ AB⊥平面 BCD,∴ AB⊥ BC, AB⊥ BD.
∵△ BCD是正三角形,且 AB= BC= a,∴ AD= AC=
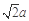 .
.
设 G为 CD的中点,则 CG=
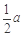 ,
AG=
,
AG=
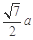 .
.
∴
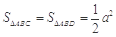 ,
,
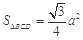 ,
,
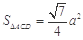 .
.
三棱锥 D- ABC的表面积为
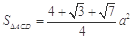 .
.
(2)取 AC的中点 H,∵ AB= BC,∴ BH⊥ AC.
∵ AF=3 FC,∴ F为 CH的中点.
∵ E为 BC的中点,∴ EF∥ BH.则 EF⊥ AC.
∵△ BCD是正三角形,∴ DE⊥ BC.
∵ AB⊥平面 BCD,∴ AB⊥ DE.
∵ AB∩ BC= B,∴ DE⊥平面 ABC.∴ DE⊥ AC.
∵ DE∩ EF= E,∴ AC⊥平面 DEF.
(3)存在这样的点 N,当 CN=
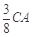 时,
MN∥平面
DEF.
时,
MN∥平面
DEF.
连 CM,设 CM∩ DE= O,连 OF.由条件知, O为△ BCD的重心, CO=
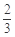 CM.
CM.
∴当 CF=
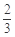 CN时,
MN∥
OF.∴
CN=
CN时,
MN∥
OF.∴
CN=
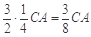
点评:题考查棱锥的结构特征,证明线面垂直,线面平行,考查逻辑思维能力,是中档题.
【简答题】

[9/2000](1)如图所示,证明命题“ a是平面 π内的一条直线, b是 π外的一条直线( b不垂直于 π), c是直线 b在 π上的投影,若 a⊥ b,则 a⊥...
参考答案:
|
(1)见解析(2)逆命题为:
a是平面
π内的一条直线,
b是
π外的一条直线(
b不垂直于
π),
c是直线
b在
π上的投影,若
a⊥
c,则
a⊥
b.真命题
|
参考解析:
(1)记
c∩
b=
A,
P为直线
b上异于点
A的任意一点,过
P作
PO⊥
π,垂足为
O,则
O∈
c.
因为 PO⊥ π, a⊂ π,
所以直线 PO⊥ a.
又 a⊥ b, b⊂平面 PAO, PO∩ b= P,
所以 a⊥平面 PAO.
又 c⊂平面 PAO,
所以 a⊥ c.
(2)逆命题为: a是平面 π内的一条直线, b是 π外的一条直线( b不垂直于 π), c是直线 b在 π上的投影,若 a⊥ c,则 a⊥ b.逆命题为真命题.
因为 PO⊥ π, a⊂ π,
所以直线 PO⊥ a.
又 a⊥ b, b⊂平面 PAO, PO∩ b= P,
所以 a⊥平面 PAO.
又 c⊂平面 PAO,
所以 a⊥ c.
(2)逆命题为: a是平面 π内的一条直线, b是 π外的一条直线( b不垂直于 π), c是直线 b在 π上的投影,若 a⊥ c,则 a⊥ b.逆命题为真命题.
【简答题】

[10/2000]设 【图片】是空间三条直线, 【图片】是空间两个平面,则下列命题中,逆命题不正确的是( ) A.当 【图片】时,若 ...
参考答案:
|
B
|
参考解析:
分别写出其逆命题再判断,A、由面面平行的性质定理判断.B、也可能平行C、由三垂线定理判断.D、由线面平行的判定定理判断.
A、其逆命题是:当c⊥α时,或α∥β,则c⊥β,由面面平行的性质定理知正确.
B、其逆命题是:当b⊂α,若α⊥β,则b⊥β,也可能平行,相交.不正确.
C、其逆命题是当b⊂α,且c是a在α内的射影时,若a⊥b,则b⊥c,由三垂线定理知正确.
D、其逆命题是当b⊂α,且c⊄α时,若b∥c,则c∥α,由线面平行的判定定理知正确.
故选B
点评:解决该试题的关键是熟练运用线面平行的判定定理和性质定理,和线面垂直的判定定理和性质定理的运用。