
下载APP

参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】一顾客需配音信个眼镜镜度为+5.00DS/+1.00DC*90,其隐形眼镜用等效球面矫正散光,应配隐形眼镜镜度为()DS。
A.
A+6.00
B.
B.+5.75
C.
C.+5.50
D.
D.+5.00
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
相关题目:

【判断题】大地高是沿法线到参考椭球面的距离。
A.
正确
B.
错误
【判断题】若 为球面 的外侧,则 等于( ).
A.
正确
B.
错误
【单选题】一顾客需配音信个眼镜镜度为+5.00DS/+1.00DC*90,其隐形眼镜用等效球面矫正散光,应配隐形眼镜镜度为()DS。
A.
A+6.00
B.
B.+5.75
C.
C.+5.50
D.
D.+5.00
【单选题】带状光检影时在球面性屈光不正中不存在()。
A.
逆动现象
B.
中和现象
C.
剪动现象
D.
顺动现象
【单选题】设 是椭球面 ,则 ()
A.
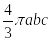
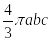
B.


C.
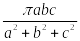
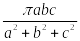
D.
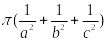
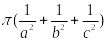
【单选题】参考椭球面和( )是大地测量计算的基准。
A.
铅垂线
B.
投影线
C.
法线
D.
平行线
【单选题】上半球面 和锥面 所围的立体在 xOy 面上的投影区域是( )
A.
xOy 面上区域
B.
xOy 面上区域
C.
xOy 面上区域
D.
xOy 面上区域
【单选题】,其中是上半椭球面的上侧面
A.
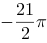
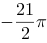
B.


C.
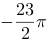
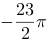
D.
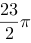
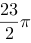
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
【单选题】精车球面时应( )。
A.
提高主轴转速
B.
提高进给速度
C.
提高中滑板进给量
D.
提高小滑板进给量

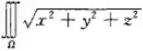 dV,其中Ω是由上半球面z=
dV,其中Ω是由上半球面z=
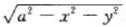 和圆锥面z=
和圆锥面z=
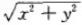 所围成的空间闭区域。
所围成的空间闭区域。
