下载APP

【单选题】


设f(x)在(0,+∞)上是单调递增函数,当n∈N*时,f(n)∈N*,且f[f(n)]=2n+1,则( )
A.
f(1)=3,f(2)=4
B.
f(1)=2,f(2)=3
C.
f(2)=4,f(4)=5
D.
f(2)=3,f(3)=4
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【简答题】已知奇函数f(x)是定义在(-1,1)上的增函数,若f(m-1)+f(2m-1)≤0,则m的取值范围是( )
A.
(-∞, 2 3 )
B.
(-∞, 2 3 ]
C.
(0, 2 3 )
D.
(0, 2 3 ]
【简答题】f(x),g(x)都是定义在R上的单调递增函数,f(x)>0,g(x)<0,则 f(x) g(x) ( )
A.
大于0,单调递增
B.
小于0,单调递减
C.
小于0,单调递增
D.
小于0,单调性无法确定
【单选题】若偶函数f(x)在(-∞,-1]上是增函数,则( )
A.
f(-1.5)<f(-1)<f(2)
B.
f(-1)<f(-1.5)<f(2)
C.
f(2)<f(-1)<f(-1.5)
D.
f(2)<f(-1.5)<f(-1)
相关题目:

【判断题】在给定的定义域范围内,函数一阶导数大于0,则函数在此区间内是增函数。
A.
正确
B.
错误
【单选题】下列四个函数中,在(0,1)上为增函数的是
A.
y=sinx
B.
y=-log2x
C.
y=( )x
)x
 )x
)xD.
y=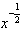
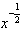
【简答题】已知奇函数f(x)是定义在(-1,1)上的增函数,若f(m-1)+f(2m-1)≤0,则m的取值范围是( )
A.
(-∞, 2 3 )
B.
(-∞, 2 3 ]
C.
(0, 2 3 )
D.
(0, 2 3 ]
【简答题】f(x),g(x)都是定义在R上的单调递增函数,f(x)>0,g(x)<0,则 f(x) g(x) ( )
A.
大于0,单调递增
B.
小于0,单调递减
C.
小于0,单调递增
D.
小于0,单调性无法确定
【单选题】若偶函数f(x)在(-∞,-1]上是增函数,则( )
A.
f(-1.5)<f(-1)<f(2)
B.
f(-1)<f(-1.5)<f(2)
C.
f(2)<f(-1)<f(-1.5)
D.
f(2)<f(-1.5)<f(-1)
【单选题】计算绝对值的函数是()
A.
abs
B.
round
C.
sqr
D.
int
【单选题】函数Mid("123456789",3,4)返回的值是______。
A.
123
B.
1234
C.
3456
D.
456
【单选题】考察知识点【隐函数求导】
A.
B.
C.
D.
D
【单选题】下列函数是偶函数且在 上是增函数的是
A.
B.
C.
【简答题】函数y= lnx x 的最大值为( )
A.
10 3
B.
e2
C.
e
D.
e-1