logo - 刷刷题
下载APP
【简答题】

已知
的一个特征向量。已知
的一个特征向量。
设矩阵A=
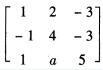的特征值有一个二重根，求a的值，并讨论矩阵A是否可相似对角化。

题目标签：相似对角化特征向量二重根
举报
如何制作自己的在线小题库
参考答案：
参考解析：
.
刷刷题刷刷变学霸
举一反三

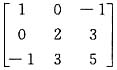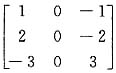【单选题】下列矩阵中，不能相似对角化的矩阵是
A.
A．
B.
.
C.
B．
D.
.
E.
C．
F.
.
G.
D．
H.
.
查看完整题目与答案

【判断题】特征向量不能是零向量
A.
正确
B.
错误
查看完整题目与答案

【简答题】设矩阵A= 1 2 3 2 3 2 - 1 2 ，求矩阵A的特征向量．
查看完整题目与答案

【简答题】设A=，求A的特征值与特征向量。
查看完整题目与答案

【单选题】设，则下列向量是A的特征向量的是
A.
[1，2，1]T．
B.
[1，-2，1]T．
C.
[2，1，2]T．
D.
[ 2，1，-2]T．
查看完整题目与答案

【简答题】设非零n维列向量α，β正交且A=αβ T ．证明：A不可以相似对角化．
查看完整题目与答案

【判断题】若Ax=λx,则λ是矩阵A的特征值,x是A的特征向量。
A.
正确
B.
错误
查看完整题目与答案

【简答题】已知矩阵A=12-14，向量a=74．（1）求矩阵A的特征值λ1、λ2和特征向量α1、α2；（2）求A5α的值．
查看完整题目与答案

【简答题】已知A＝，求A的特征值、特征向量，并判断A能否相似对角化，说明理由．
查看完整题目与答案

【简答题】线性代数。设矩阵A=1、0、0;1、2、2;1、1、3,问矩阵A可否相似对角化?若能相似对角化,则求可逆阵P,使P^(－1)AP为对角阵。
查看完整题目与答案