
下载APP

【简答题】


线性代数。设矩阵A=1、0、0;1、2、2;1、1、3,问矩阵A可否相似对角化?若能相似对角化,则求可逆阵P,使P^(-1)AP为对角阵。
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】n阶方阵A相似于对角阵的充分必要条件是( ).
A.
A有n个互异的特征向量.
B.
A有n个互异的特征值.
C.
对A的每个
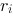 重特征值
重特征值
 ,有
,有
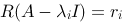
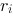 重特征值
重特征值
 ,有
,有
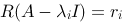
D.
对A的每个
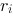 重特征值
重特征值
 ,有
,有
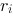 个线性无关的特征向量.
个线性无关的特征向量.
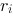 重特征值
重特征值
 ,有
,有
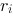 个线性无关的特征向量.
个线性无关的特征向量.
