
下载APP

【简答题】


设α 1 ,α 2 ,α 3 为四维列向量组,α 1 ,α 2 线性无关,α 3 =3α 1 +2α 2 ,A=(α 1 ,α 2 ,α 3 ),求Ax=0的一个基础解系.
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】n维向量组α 1 ,α 2 ,…,α 3 (3≤s≤n)线性无关的充要条件是 ( )
A.
存在一组全为零的数k 1 ,k 2 ,…,k s ,使k 1 α 1 +k 2 α 2 +…+k s α s =0
B.
α 1 ,α 2 ,…,α s 中任意两个向量都线性无关
C.
α 1 ,α 2 ,…,α s 中任意一个向量都不能由其余向量线性表出
D.
存在一组不全为零的数k 1 ,k 2 ,…,k s ,使k 1 α 1 +k 2 α 2 +…+k s α s ≠0
【单选题】设n维向量组 , ,... 线性无关,则( )
A.
向量组中任一向量均可由其余向量线性表示
B.
向量组中只有一个向量可由其余向量线性表示
C.
向量组中存在某一个向量可有其余向量线性表示
D.
以上说法都不正确
【单选题】设A=(α 1 ,α 2 ,…,α m ),其中α 1 ,α 2 ,…,α m 是n维列向量,若对于任意不全为零的常数k 1 ,k 2 ,…,k m ,皆有k 1 α 1 +k 2 α 2 +…+k m α m ≠0,则( ).
A.
m>n
B.
m=n
C.
存在m阶可逆阵P,使得AP=
D.
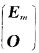
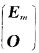
E.
D.若AB=O,则B=O

