下载APP

【简答题】


设n维列向量α 1 ,α 2 ,…,α n-1 线性无关,且与非零向量β 1 ,β 2 都正交.证明β 1 ,β 2 线性相关,α 1 ,α 2 ,…,α n-1 ,β 1 线性无关.
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】线性相关系数可以表达的两变量间( )。
A.
线性相关程度、线性相关方向、因果关系
B.
线性相关程度、因果关系
C.
线性相关方向、因果关系
D.
线性相关程度、线性相关方向
【单选题】设A=(α 1 ,α 2 ,…,α m ),其中α 1 ,α 2 ,…,α m 是n维列向量,若对于任意不全为零的常数k 1 ,k 2 ,…,k m ,皆有k 1 α 1 +k 2 α 2 +…+k m α m ≠0,则( ).
A.
m>n
B.
m=n
C.
存在m阶可逆阵P,使得AP=
D.
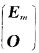
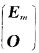
E.
D.若AB=O,则B=O
【单选题】设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于[ ]
A.
以a,b为两边的三角形面积
B.
以b,c为两边的三角形面积
C.
以a,b为邻边的平行四边形的面积
D.
以b,c为邻边的平行四边形的面积
【简答题】已知 a 、 b 为两个非零向量,有以下命题:① a 2= b 2 ② a • b = b 2 ③| a |=| b |且 a ∥ b ,其中可以作 a = b 的必...
A.
②
B.
①③
C.
②③
D.
①②③
相关题目:

【判断题】一个向量空间中若含有非零向量,那么一定含有无穷多个非零向量。( )
A.
正确
B.
错误
【单选题】线性相关系数可以表达的两变量间( )。
A.
线性相关程度、线性相关方向、因果关系
B.
线性相关程度、因果关系
C.
线性相关方向、因果关系
D.
线性相关程度、线性相关方向
【单选题】下列命题中: ①若,则或; ②若不平行的两个非零向量,满足,则;③若与平行,则;④若∥,∥,则∥;其中真命题的个数是()
A.
1
B.
2
C.
3
D.
4
【单选题】设A=(α 1 ,α 2 ,…,α m ),其中α 1 ,α 2 ,…,α m 是n维列向量,若对于任意不全为零的常数k 1 ,k 2 ,…,k m ,皆有k 1 α 1 +k 2 α 2 +…+k m α m ≠0,则( ).
A.
m>n
B.
m=n
C.
存在m阶可逆阵P,使得AP=
D.
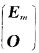
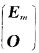
E.
D.若AB=O,则B=O
【单选题】设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于[ ]
A.
以a,b为两边的三角形面积
B.
以b,c为两边的三角形面积
C.
以a,b为邻边的平行四边形的面积
D.
以b,c为邻边的平行四边形的面积
【单选题】设a,b,c为非零向量,且 ,则 ( ).
A.
0
B.
1
C.
3
D.
5
【简答题】已知 a 、 b 为两个非零向量,有以下命题:① a 2= b 2 ② a • b = b 2 ③| a |=| b |且 a ∥ b ,其中可以作 a = b 的必...
A.
②
B.
①③
C.
②③
D.
①②③
【单选题】非零向量 满足 ,则有
A.
∥
B.
λ (λ为实数)
C.
⊥
D.
+ =
【单选题】已知非零向量、满足向量+与向量-的夹角为,那么下列结论中一定成立的是( )
A.
 =
=

 =
=

B.
|
 |=|
|=|
 |,
|,
 |=|
|=|
 |,
|,C.
 ⊥
⊥

 ⊥
⊥

D.
 ∥
∥

 ∥
∥

【单选题】设 是两个非零向量,则下列结论不正确的是
A.
若存在一个实数
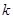 满足
满足
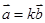 ,则
,则
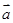 与
与
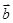 共线
共线
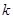 满足
满足
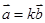 ,则
,则
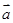 与
与
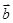 共线
共线B.
若
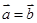 ,则
,则
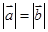
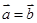 ,则
,则
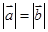
C.
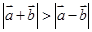
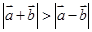
D.
若
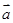 与
与
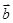 为两个方向相同的向量,则
为两个方向相同的向量,则
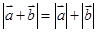
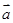 与
与
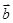 为两个方向相同的向量,则
为两个方向相同的向量,则