
下载APP

参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】设 p(x)为 F[x]中的不可约多项式,f(x),g(x)∈F[x],则错误命题是( )。
A.
若 p(x)不整除 f(x),则(p(x),f(x))=1,
B.
若(p(x),f(x))≠1,则 p(x)|f(x)
C.
若 p(x)|f(x)g(x)且 p(x)不整除 f(x),则(p(x),g(x))≠1
D.
若 p(x)|f(x)g(x),则(f(x),g(x))=1
相关题目:

【判断题】在复数域C中,x^2+1是不可约多项式。
A.
正确
B.
错误
【单选题】在复数域C中,属于不可约多项式的是
A.
x^2-1
B.
x^4-1
C.
x^2+1
D.
x+1
【单选题】设 p(x)为 F[x]中的不可约多项式,f(x),g(x)∈F[x],则错误命题是( )。
A.
若 p(x)不整除 f(x),则(p(x),f(x))=1,
B.
若(p(x),f(x))≠1,则 p(x)|f(x)
C.
若 p(x)|f(x)g(x)且 p(x)不整除 f(x),则(p(x),g(x))≠1
D.
若 p(x)|f(x)g(x),则(f(x),g(x))=1
【判断题】数域上的任意元二次多项式都是数域上的一个元二次型。
A.
正确
B.
错误
【单选题】下列多项式中,不能进行因式分解的是[ ]
A.
﹣a2+b2
B.
﹣a2﹣b2
C.
﹣a2﹣b2+2ab
D.
a2﹣3a+2
【单选题】生成多项式 G ( X ) =X 4 +X 3 +1,转化成二进制编码形式为
A.
11000
B.
11111
C.
11001
D.
10001
【单选题】p(x)是R[x]上不可约多项式,如果p(x)的复根c是实数,那么p(x)是什么多系式?
A.
零次多项式
B.
四次多项式
C.
三次多项式
D.
一次多项式
【判断题】域必定是整环
A.
正确
B.
错误
【单选题】在有理数域Q中,属于可约多项式的是()。
A.
x^2+1
B.
x^2-1
C.
x^2-3
D.
x^2-5

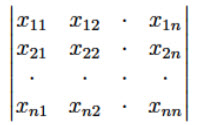 是整环R[x11,x12,…,xn1,xn2,…,xnn]中不可约多项式。
是整环R[x11,x12,…,xn1,xn2,…,xnn]中不可约多项式。
