
下载APP

【判断题】


如果一个方阵A可以相似对角化,那么与它相似的对角矩阵对角线上的元素就是A的特征值, 且把A变成对角矩阵的相似变换矩阵P,就是由A的所有线性无关的特征向量组成的。
A.
正确
B.
错误
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】对三对角矩阵A采用压缩存储的方法将所有非零元素存放于一个一维数组B[3n-2]中,某非零元素aij在B中位置是____________。
A.
2×i+j-2
B.
2×i+j+2
C.
2×i+j-3
D.
2×i+j-1


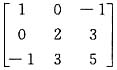 .
. .
.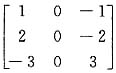 .
. .
.