
下载APP

【简答题】


利用柱面坐标计算下列三重积分: (1),其中Ω是由上半球面与旋转抛物面z=x2+y2所围成的闭区域. 利用柱面坐标计算下列三重积分:
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】设S是抛物面z=x2+y2在第一卦限中介于z=0,z=2之间部分的下侧,则∫∫szdxdy=()
A.
-∫02πdθ∫02ρ3dρ
B.
-∫0π/2dθ∫0√2ρ3dρ
C.
∫0π/4dθ∫0√2ρ2dρ
D.
-∫0π/2dθ∫0√2ρ2dρ
【单选题】双曲抛物面$z=xy$被圆柱面${{x}^{2}}+{{y}^{2}}={{a}^{2}}$截下部分的面积为( )
A.
$\frac{2\pi }{3}[{{(1+a)}^{3/2}}+1]$
B.
$\frac{2\pi }{3}[{{(1+a)}^{3/2}}-1]$
C.
$\frac{2\pi }{3}[{{(1+a)}^{2/3}}+1]$
D.
$\frac{2\pi }{3}[{{(1+a)}^{2/3}}-1]$
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
【单选题】椭圆抛物面z=3x^2-4y^2与平面z=12的交线是
A.
3x^2-4y^2=12
B.
3x^2-4y^2=12,z=0
C.
3x^2-4y^2=12,z=12
D.
不存在
相关题目:

【单选题】设S是抛物面z=x2+y2在第一卦限中介于z=0,z=2之间部分的下侧,则∫∫szdxdy=()
A.
-∫02πdθ∫02ρ3dρ
B.
-∫0π/2dθ∫0√2ρ3dρ
C.
∫0π/4dθ∫0√2ρ2dρ
D.
-∫0π/2dθ∫0√2ρ2dρ
【判断题】旋转抛物面z=x2+y2-1在点(2, 1, 4)处的切平面方程为 。
A.
正确
B.
错误
【单选题】双曲抛物面$z=xy$被圆柱面${{x}^{2}}+{{y}^{2}}={{a}^{2}}$截下部分的面积为( )
A.
$\frac{2\pi }{3}[{{(1+a)}^{3/2}}+1]$
B.
$\frac{2\pi }{3}[{{(1+a)}^{3/2}}-1]$
C.
$\frac{2\pi }{3}[{{(1+a)}^{2/3}}+1]$
D.
$\frac{2\pi }{3}[{{(1+a)}^{2/3}}-1]$
【判断题】+ =z为抛物面
A.
正确
B.
错误
【判断题】旋转抛物面 与柱面 的交线是一个圆
A.
正确
B.
错误
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
【单选题】椭圆抛物面z=3x^2-4y^2与平面z=12的交线是
A.
3x^2-4y^2=12
B.
3x^2-4y^2=12,z=0
C.
3x^2-4y^2=12,z=12
D.
不存在
【判断题】方程 所表示的曲面为椭圆抛物面.( )
A.
正确
B.
错误
【判断题】双曲抛物面是直纹面.
A.
正确
B.
错误
【单选题】设是由抛物面和半球面所围成的空间闭区域,函数在上连续,记,,则 .
A.
正确
B.
错误
【单选题】设曲面为抛物面位于面以上的部分,计算积分( )。
A.
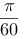
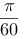
B.


C.
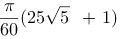
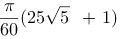
D.


【单选题】单层椭圆抛物面网壳的跨度不宜大于( )m。
A.
30
B.
50
C.
60
D.
80

