
下载APP

【简答题】


设H为可分Hilbert空间,{u n }为H的标准正交基,{k n }为有界纯量列求证: , x∈H 定义了H上的正规算子[这样的算子被称为 对角算子 ]。求A的特征值和谱。
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】设 a , b 是一组非正交的基底,为得到正交基底,可在集合 { a +t b |t∈R} 中找一个向量与 a 组成一组正交基底,根据上述要求,若 a =(1,2) , b =(2,3) ,则t的值为( )
A.
- 3 8
B.
- 5 11
C.
- 5 8
D.
- 7 9
【多选题】设【图片】是n维欧氏空间V的正交变换,且【图片】是V的标准正交基,则下列叙述正确的有( )。
A.
也 是V 的标准正交基。
B.
在基 下的矩阵是正交矩阵。
C.
是 欧氏空间V 到自身的同构映射。
D.
的行列式是 1或-1。
相关题目:

【判断题】欧式空间两组标准正交基之间的过渡矩阵是正交矩阵?
A.
对
B.
错
【单选题】求h满足矩阵的列向量组构成2维复向量空间的一组标准正交基。
A.
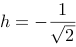
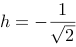
B.
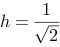
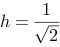
C.
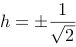
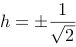
D.
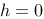
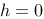
【判断题】设A是n阶正交矩阵,则A的行、列向量组都是R^n的标准正交基。
A.
正确
B.
错误
【判断题】空间【图片】中的标准正交基是唯一的.
A.
正确
B.
错误
【判断题】第二类正交变换在标准正交基下的矩阵行列式等于-1。
A.
正确
B.
错误
【单选题】任何Hilbert空间都具有标准正交基.
A.
正确
B.
错误
【判断题】正交变换在标准正交基下的矩阵为正交矩阵。
A.
正确
B.
错误
【单选题】设 a , b 是一组非正交的基底,为得到正交基底,可在集合 { a +t b |t∈R} 中找一个向量与 a 组成一组正交基底,根据上述要求,若 a =(1,2) , b =(2,3) ,则t的值为( )
A.
- 3 8
B.
- 5 11
C.
- 5 8
D.
- 7 9
【多选题】n维欧氏空间 中标准正交基具有的性质:
A.
是一个非零向量组
B.
其中每个向量都是单位向量
C.
是唯一的
D.
任两个相异向量内积为零
【多选题】设【图片】是n维欧氏空间V的正交变换,且【图片】是V的标准正交基,则下列叙述正确的有( )。
A.
也 是V 的标准正交基。
B.
在基 下的矩阵是正交矩阵。
C.
是 欧氏空间V 到自身的同构映射。
D.
的行列式是 1或-1。

