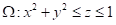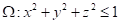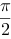下载APP
【简答题】
应用高斯公式计算三重积分
（xy+yz+zx）dxdydz，其中V是由x≥0，y≥0，0≤z≤1与x
2
+y
2
≤1所确定的空间区域。
举报
题目标签：
三重积分
高斯公式
空间区域
参考答案：
参考解析：
刷刷题刷刷变学霸
举一反三
【简答题】设Ω为，则三重积分化为球坐标系下的三次积分为______．
查看完整题目与答案
【多选题】下列空间闭区域中，能使三重积分的值为0的是（ ）.
A.
B.
C.
D.
查看完整题目与答案
【单选题】高斯公式中P、Q、R在空间闭区域上具有
A.
连续
B.
偏导数存在
C.
可微分
D.
一阶连续偏导数
查看完整题目与答案
【简答题】求三重积分：。Ω：x2+y2≤2z，z≤2。
查看完整题目与答案
【判断题】透镜成像的高斯公式为:
A.
正确
B.
错误
查看完整题目与答案
【简答题】利用高斯公式计算曲面积分： 其中Σ为平面x2+y2+z2=a2的外侧。
查看完整题目与答案
【简答题】如何利用对称性来简化三重积分的计算?
查看完整题目与答案
【简答题】设门是由锥面z=围成的空间区域，∑是Ω的整个边界的外侧，则xdydz+ydzdx+zdxdy=_________．
查看完整题目与答案
【单选题】设是由球面所围成的闭区域，则三重积分（ ）。
A.
B.
C.
D.
查看完整题目与答案
【简答题】设积分区域：Ω0≤x≤1，0≤y≤1，0≤z≤1，则三重积分______.
查看完整题目与答案
（xy+yz+zx）dxdydz，其中V是由x≥0，y≥0，0≤z≤1与x2+y2≤1所确定的空间区域。
