
下载APP

【单选题】


函数 z=f(x,y) 在点(x0,y0) 处具有偏导数是它在该点存在全微分的:
A.
必要而非充分条件
B.
充分而非必要条件
C.
充分必要条件
D.
既非充分又非必要条件
参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】已知二元函数$z(x,y)=\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}$,则$z(x,y)$的全微分$\text{d}z=$( )
A.
$\frac{x}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
B.
$-\frac{x}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
C.
$-\frac{y}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
D.
$\frac{y}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
相关题目:

【单选题】函数 在点(0,0)的两个偏导数是否存在?在点(0,0)是否可微?()
A.
偏导不存在,不可微
B.
偏导不存在,可微
C.
偏导存在,不可微
D.
偏导存在,可微
【单选题】设函数,则偏导数
A.
-1
C.
1
D.
2
【单选题】设函数 的全微分 ,则点 ( )
A.
不是
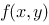 的极值点
的极值点
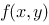 的极值点
的极值点B.
不是
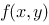 的连续点
的连续点
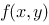 的连续点
的连续点C.
是
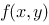 的极大值点
的极大值点
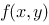 的极大值点
的极大值点D.
是
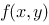 的极小值点
的极小值点
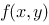 的极小值点
的极小值点【单选题】微分调节的输入和输出的关系表示为()。
A.
P=KiC
B.
P=At/Ti
C.
P=Td×de/dt
D.
P=e/δ
【判断题】设具有连续偏导数,且,令,则的值为。
A.
正确
B.
错误
【单选题】函数 在点 处具有两个偏导数 , 是函数在该点存在全微分的( )。
A.
充分条件
B.
充要条件
C.
必要条件
D.
既不是充分条件,又不是必要条件
【单选题】已知为某函数的全微分,则a等于
A.
一1.
B.
0.
C.
1.
D.
2.
【单选题】已知二元函数$z(x,y)=\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}$,则$z(x,y)$的全微分$\text{d}z=$( )
A.
$\frac{x}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
B.
$-\frac{x}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
C.
$-\frac{y}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$
D.
$\frac{y}{{{({{x}^{2}}+{{y}^{2}})}^{3/2}}}(y\text{d}x-x\text{d}y)$

