下载APP
【简答题】
设X是一个内积空间，(.,.)为内积，
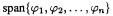是x的一个n空间．f∈x，
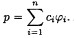对
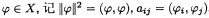，1≤i，j≤n，b i =(f，
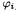)，1≤i≤n，矩阵A=[a ij ]，b=(b 1 ，b 2 ，…，b n ) T ． 1)证明：线性方程组Ax=b存在唯一解； 2)如果P满足‖f-p‖=
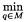‖f-q‖证明：c 1 ，c 2 ，…，c n 是线性方程组Ax=b的解．
参考答案：
参考解析：
刷刷题刷刷变学霸
举一反三
【单选题】以下哪个是线性方程组\(\begin{pmatrix} 1 & -1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{pmatrix} \mathbf{x} = 0\)的解
A.
\(\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\)
B.
\(\begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}\)
C.
\(\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}\)
D.
\(\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\)