下载APP
【简答题】
设∑un、∑vn为正项级数，且存在正数N0，对一切n>N0，有
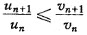;证明：若级数∑vn收敛，则级数∑un也收敛；若∑un发散，则∑vn也发散。
参考答案：
参考解析：
刷刷题刷刷变学霸
举一反三
【单选题】关于判别正项级数【图片】的敛散性的说法正确的是（ ）
A.
应用比值审敛法证明该级数发散
B.
应用根值审敛法证明该级数发散
C.
应用根值审敛法证明该级数收敛
D.
应用比值审敛法证明该级数收敛
【单选题】在正数等比数列 { a n } 中 , a n + 1 < a n , a 2 a 8=6 , a 4 + a 6=5 , 则=
A.
1.4
B.
1.3
C.
1.2
D.
1.5
相关题目：
【判断题】级数是减速器传动齿轮的段数。（）
A.
正确
B.
错误
【单选题】正项级数 的部分和数列 有上界是级数 收敛的( )
A.
充要条件
B.
必要条件
C.
充分条件
D.
无关条件
【单选题】已知各项均为正数的等比数列{}，=5，=10，则=（）
A.
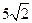
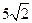
B.
7
C.
6
D.
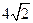
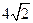
【单选题】关于判别正项级数【图片】的敛散性的说法正确的是（ ）
A.
应用比值审敛法证明该级数发散
B.
应用根值审敛法证明该级数发散
C.
应用根值审敛法证明该级数收敛
D.
应用比值审敛法证明该级数收敛
【单选题】正项级数满足条件（ ）必收敛.
A.
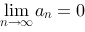
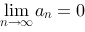
B.
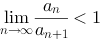
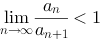
C.
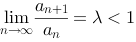
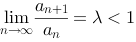
D.
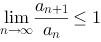
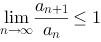
【单选题】用性质判断下列级数的敛散性:
A.
收敛, 1
B.
发散
C.
收敛, n
D.
收敛, 2
【单选题】正项级数的部分和数列有界是该数列收敛的( )
A.
充分条件
B.
必要条件
C.
充要条件
D.
以上都不是
【判断题】设 是正项级数,设 ,则当 (或 )时,级数 发散.
A.
正确
B.
错误
【单选题】在正数等比数列 { a n } 中 , a n + 1 < a n , a 2 a 8=6 , a 4 + a 6=5 , 则=
A.
1.4
B.
1.3
C.
1.2
D.
1.5
【判断题】由敛散性的判别方法知正项级数 的敛散性为收敛
A.
正确
B.
错误
【单选题】设为正项级数，下列结论中正确的是______． (
A.
若，则级数收敛 (
B.
若存在非零常数λ，使，则级数发散 (
C.
若
【判断题】倾斜改正数一定是个负值。()
A.
正确
B.
错误