
下载APP

【简答题】


3.如果三重积分的被积函数f(x,y,z)是三个函数f1(x)、f2(y)、f3(z)的乘积,即f(x,y,z)=f1(x)·f2(y)·f3(z).积分区域Ω={(x,y,z)|a≤x≤b,c≤y≤d,l≤z≤m},证明这个三重积分等于三个单积分的乘积,即

参考答案:


参考解析:




刷刷题刷刷变学霸
举一反三

【单选题】设积分区域D:|x|≤a,|y|≤b,且f(x,y)在D上连续,则 ( )
A.
其中D 1 :0≤x≤a,0≤y≤b;
B.
0:
C.
.其中D 2 :-a≤x≤0,0≤y≤b;
D.
以上三种都不对.
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
相关题目:

【单选题】设积分区域G是由坐标面和平面x+2y+3z=6所围成的,则三重积分 ( )
A.
6
B.
12
C.
18
D.
36
【单选题】设积分区域D:x2+y2≤3,则二重积分=( )
A.
-9π
B.
-3π
C.
3π
D.
9π
【判断题】定积分的值不仅取决于被积函数与积分上下限,还与积分变量的记号有关。
A.
正确
B.
错误
【判断题】计算三重积分时,如果被积函数关于某变量是奇函数,则此三重积分一定等于零
A.
正确
B.
错误
【单选题】设为立方体:,则三重积分=( )
A.
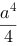
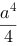
B.
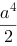
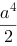
C.


D.
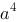
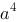
【单选题】设积分区域D:|x|≤a,|y|≤b,且f(x,y)在D上连续,则 ( )
A.
其中D 1 :0≤x≤a,0≤y≤b;
B.
0:
C.
.其中D 2 :-a≤x≤0,0≤y≤b;
D.
以上三种都不对.
【判断题】如果定积分的被积函数含有未知参数,则求积公式不能计算这样的定积分问题。( )
A.
正确
B.
错误
【单选题】设空间闭区域Ω由曲面z=√(1-x2-y2)及z=√x2+y2可围成,则三重积分∫∫∫Ω(x2+y2+z2)dxdydz=()
A.
∫02πdθ∫0π/2sinφdφ∫01rdr
B.
∫02πdθ∫0π/4sinφdφ∫01r4dr
C.
∫02πdθ∫0π/2sinφdφ∫01r2dr
D.
∫02πdθ∫0π/4sinφdφ∫01r3dr
【单选题】当被积函数是( )时,用分部积分法。
A.
基本初等函数
B.
简单函数
C.
两类函数相乘
D.
复合函数

