基本不等式及其应用题库 - 考试题库

【简答题】

[1/2000]设x∈R+且x2+ y22=1，求x 1+y2的最大值．

参考答案：

∵x＞0，
∴x

1+y2

=

2

?

x2(

1

2

+

y2

2

)

≤

2

[x2+(

1

2

+

y2

2

)]

2

，
又x²+（

1

2

+

y2

2

）=（x²+

y2

2

）+

1

2

=

3

2

∴x

1+y2

≤

2

（

1

2

×

3

2

）=

3

2

4

即(x

1+y2

)max=

3

2

4

．

参考解析：

无

【简答题】

[2/2000]设△ABC的内角A，B，C的对边分别为a，b，c。已知b2+c2=a2+bc，求：（Ⅰ）A的大小；（Ⅱ）若a=2，求△ABC面积的最大值。

参考答案：

解：（Ⅰ）由余弦定理，

，
故cosA=

，
又A

，
所以A=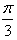

；
（Ⅱ）a=2，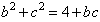
∴

，
又

，
∴

，
∴bc≤4，
∴

，
当且仅当b=c=2时取“=”，
所以△ABC面积的最大值

。

参考解析：

无

【简答题】

[3/2000]下列结论正确的是 A当【图片】 B 【图片】C 【图片】 D 【图片】

参考答案：

B

参考解析：

无

【简答题】

[4/2000]在算式“1×□+4×□=30”的两个□中，分别填入两个自然数，使它们的倒数之和最小，则这两个数的和为______．

参考答案：

设1×m+4n=30，m、n∈N₊，则m=30-4n，其中1≤n≤7．
所以y=

1

m

+

1

n

=

1

30-4n

+

1

n

=

3(10-n)

n(30-4n)

，
则

1

y

=

n(30-4n)

3(10-n)

=

40n-4n2-10n

3(10-n)

=

4n(10-n)-10n

3(10-n)

=

4n

3

-

10n

3(10-n)

=

4n

3

+

10(10-n)-100

3(10-n)

=

4n

3

-

100

3(10-n)

+

10

3

=

-4(10-n)+40

3

-

100

3 (10-n)

+

10

3

=-

4

3

[（10-n）+

25

10-n

]+

50

3

≤-

4

3

×2×

25

+

50

3

=

10

3

．
当10-n=

25

10-n

时取等号，即

1

y

取得最大值，y取得最小值．
解得n=5，则m=10．所以m+n=15．
故答案为15．

参考解析：

无

【简答题】

[5/2000]若正实数x，y满足2x+y+6=xy，则xy的最小值是（）．

参考答案：

18

参考解析：

无

【简答题】

[6/2000]设a＞0，b＞0，则以下不等式中不恒成立的是（　　） A．(a+b)( 1a+ 1b)≥4B．a3+b3≥2ab2C．a2+b2+2≥2a+2bD．

参考答案：

∵a＞0，b＞0，
∴A．(a+b)(

1

a

+

1

b

)≥2

参考解析：

1a

【简答题】

[7/2000]已知【图片】为 ...

参考答案：

参考解析：

解：因为

为

【简答题】

[8/2000]设正数x，y满足log2（x+y+3）=log2x+log2y，则x+y的取值范围是（　　） A．（0，6]B．[6，+∞）C．[1+7，+∞）D．（...

参考答案：

由正数x，y满足log₂（x+y+3）=log₂x+log₂y，∴x+y+3=xy，
而xy≤(

x+y

2

)2，则x+y+3≤

(x+y)2

4

．当且仅当x=y＞0时取等号．
令x+y=t，则t+3≤

t2

4

化为t²-4t-12≥0，解得t≥6或t≤-2．
∵t＞0，∴取t≥6．
故选B．

参考解析：

x+y2

【简答题】

[9/2000]已知a＞0，b＞0，a，b的等差中项是【图片】，且α=a+ 【图片】，β=b+ 【图片】，则α+β的最小值是 [ ...

参考答案：

C

参考解析：

无

【简答题】

[10/2000]已知正数【图片】满足【图片】，则【图片】的最小值为．

参考答案：

9

参考解析：

因为

，当且仅当

即

时取等号，所以

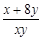的最小值为9.