
下载APP

比较法题库

题数
147
考试分类
高中数学>比较法
售价
¥15
收藏
分享
去刷题



章节目录
简介
高中数学-比较法
...更多
题目预览
【简答题】

[1/147]如果a,b都是正数,且a≠b,求证: 【图片】。
参考答案:
证明: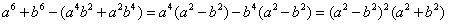 , ,∵a,b都是正数,且a≠b, ∴ 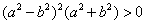 , ,∴ 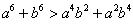 。 。 |
参考解析:
无
【简答题】

[2/147]试用分析法证明不等式 【图片】
参考答案:
|
证明见解析
|
参考解析:
用分析法证明是从要证的结论出发一直寻找使结论成立的充分条件,直到找到题目所给条件或已知的定理,公理,公式为止.
本小题应该先对要证的式子进行变形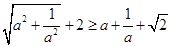 ,由于式子两边都为正数,再平方去掉根号进行证明即可
,由于式子两边都为正数,再平方去掉根号进行证明即可
证明:要证原不等式,只需证.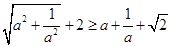 …………2分
…………2分
∵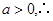 两边均大于零.
两边均大于零.
因此只需证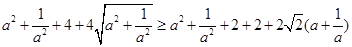 …………4分
…………4分
只需证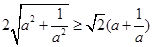 ……………6分
……………6分
只需证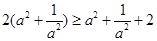 ,即证
,即证
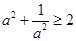 ,而
,而
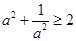 显然成立 …10分
显然成立 …10分
 原不等式成立.
原不等式成立.
本小题应该先对要证的式子进行变形
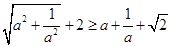 ,由于式子两边都为正数,再平方去掉根号进行证明即可
,由于式子两边都为正数,再平方去掉根号进行证明即可
证明:要证原不等式,只需证.
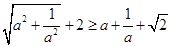 …………2分
…………2分
∵
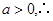 两边均大于零.
两边均大于零.
因此只需证
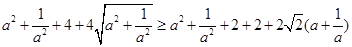 …………4分
…………4分
只需证
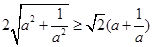 ……………6分
……………6分
只需证
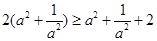 ,即证
,即证
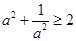 ,而
,而
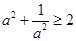 显然成立 …10分
显然成立 …10分
 原不等式成立.
原不等式成立.
【简答题】

[3/147](本题满分12分) 已知: 【图片】求证: 【图片】
参考答案:
|
.证明:
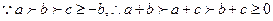 …………2分 …………2分
由于 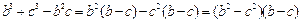
=  ………………5分 ………………5分
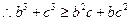 …………①………………6分 …………①………………6分
由于 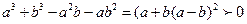
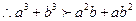 ………②……………8分 ………②……………8分
同理: 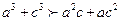 …………③……………10分 …………③……………10分
①+②+③得: 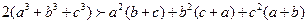
即原不等式成立………………12分 |
参考解析:
同答案
【简答题】

[4/147](选做题)证明:(1)已知x,y都是正实数,求证:x3+y3≥x2y+xy2,(2)已知a,b,c∈R+,且a+b+c=1,求证: 【图片】.
参考答案:
| 证明:(1)∵(x3+y3 )﹣(x2y+xy2)=x2 (x﹣y)+y2(y﹣x)=(x﹣y)(x2﹣y2 ) =(x+y)(x﹣y)2. ∵x,y都是正实数,∴(x﹣y)2≥0,(x+y)>0, ∴(x+y)(x﹣y)2≥0, ∴x3+y3≥x2y+xy2. (2)∵a,b,c∈R+,且a+b+c=1, ∴1=(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≤3(a2+b2+c2), ∴a2+b2+c2≥  ,当且仅当a=b=c 时,等号成立. ,当且仅当a=b=c 时,等号成立. |
参考解析:
无
【简答题】

[5/147]甲、乙两人同时从A到B。甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步。如果两人步行速度、跑步速度均相同,则 A.甲先到B B.乙先到B ...
参考答案:
| B |
参考解析:
无
【简答题】

[6/147]若0<a<b,a+b=1,则a,b,2ab,a2+b2,按从小到大的顺序排列为( )。
参考答案:
 |
参考解析:
无
【简答题】

[7/147]已知 【图片】,求证: 【图片】.
参考答案:
|
同解析
|
参考解析:
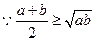 ,且
,且
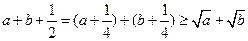 ,
,
∴
 ,
,
即
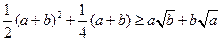 .
.
【简答题】

[8/147]设a,b是非负实数,求证: 【图片】。
参考答案:
| 证明:由a,b是非负实数, 作差得 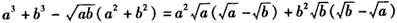 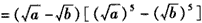 , ,当a≥b时, 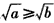 ,从而 ,从而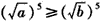 ,得 ,得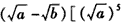 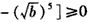 ; ;当a<b时, 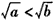 ,从而 ,从而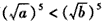 ,得 ,得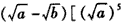 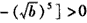 ; ;所以  。 。 |
参考解析:
无
【简答题】

[9/147]已知a>0,b>0,求证: 【图片】≥a+b。
参考答案:
解:  =(a-b)(a+b)(  )= )= (a-b)2(a+b) (a-b)2(a+b)∵a>0,b>0 ∴  。 。 |
参考解析:
无
【简答题】

[10/147]选修4—5:不等式选讲(10分): (1)已知正数a、b、c,求证: 【图片】+ 【图片】+ 【图片】≥ 【图片】(2)已知正数a、b、c,满足a 【...
参考答案:
|
证明略
|
参考解析:
证明:(1)正数a、b、c,
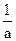 、
、
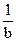 、
、
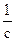 亦为正数,所以由柯西不等式得
亦为正数,所以由柯西不等式得
(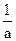 +
+
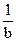 +
+
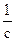 )(a+b+c)≥(
)(a+b+c)≥(
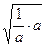 +
+
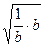 +
+
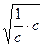 )
)
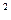 ="9 " -------3分
="9 " -------3分
“=”成立当且仅当a="b=c " -----------4分
即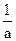 +
+
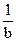 +
+
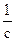 ≥
≥
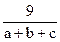 ----------5分
----------5分
(2)由(1)得
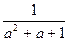 +
+
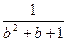 +
+
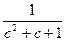 ≥
≥
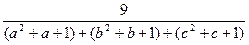 =
=
 =
=
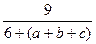 (“=”成立当且仅当a="b=c)" ---7分
(“=”成立当且仅当a="b=c)" ---7分
由均值不等式得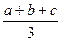
 ≤
≤
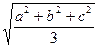 =1
=1
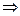 a+b+c≤3
a+b+c≤3
(“=”成立当且仅当a="b=c) " -----------9分
0< 6+(a+b+c)≤9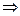
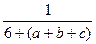 ≥
≥

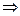
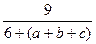 ≥1
≥1
即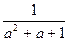 +
+
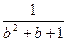 +
+
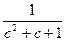 ≥1 (“=”成立当且仅当a="b=c)" --------10分
≥1 (“=”成立当且仅当a="b=c)" --------10分
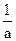 、
、
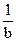 、
、
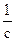 亦为正数,所以由柯西不等式得
亦为正数,所以由柯西不等式得
(
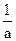 +
+
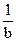 +
+
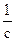 )(a+b+c)≥(
)(a+b+c)≥(
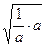 +
+
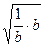 +
+
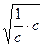 )
)
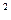 ="9 " -------3分
="9 " -------3分
“=”成立当且仅当a="b=c " -----------4分
即
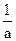 +
+
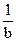 +
+
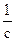 ≥
≥
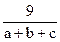 ----------5分
----------5分
(2)由(1)得
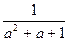 +
+
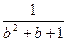 +
+
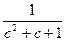 ≥
≥
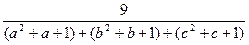 =
=
 =
=
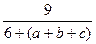 (“=”成立当且仅当a="b=c)" ---7分
(“=”成立当且仅当a="b=c)" ---7分
由均值不等式得
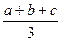
 ≤
≤
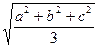 =1
=1
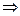 a+b+c≤3
a+b+c≤3
(“=”成立当且仅当a="b=c) " -----------9分
0< 6+(a+b+c)≤9
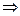
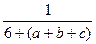 ≥
≥

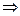
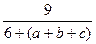 ≥1
≥1
即
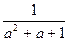 +
+
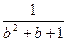 +
+
 ≥1 (“=”成立当且仅当a="b=c)" --------10分
≥1 (“=”成立当且仅当a="b=c)" --------10分