
下载APP

算法的概念题库

题数
1010
考试分类
高中数学>算法的概念
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-算法的概念
...更多
题目预览
【简答题】

[1/1010]对任意非零实数 【图片】, 【图片】,若 【图片】的运算规则如右图的程序框图所示,则 【图片】的值是____________ 【图片】
参考答案:

|
参考解析:
由程序框图知
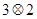 中
中
 ,则
,则
 ,故
,故
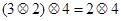 ,而
,而
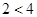 ,则
,则
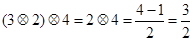 .
.
【简答题】

[2/1010]已知实数 【图片】,执行如右图所示的程序框图,则输出的 【图片】不小于55的概率为 【图片】A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
A
|
参考解析:
分析框图的特点可知,设实数x∈[0,8],经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=3此时输出x
输出的值为8x+7,令8x+7≥54,得x≥6
由几何概型得到输出的x不小于54的概率为=
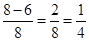 故选A.
故选A.
点评:解决程序框图中的循环结构时,一般采用先根据框图的流程写出前几次循环的结果,根据结果找规律.
【简答题】

[3/1010]程序框图(即算法流程图)如右图所示,其输出结果是( ) 【图片】A. 【图片】B. 【图片...
参考答案:
|
B
|
参考解析:
根据题意,按照程序框图的顺序进行执行,然后输出结果即可.
解:由程序框图知,循环体被执行后a的值依次为3、7、15、31、63、127,故输出的结果是127.
本题考查程序框图的识别,通过对已知框图的分析与执行,写出运算结果,属于基础题.
【简答题】

[4/1010]如图所示的流程图中,输出的结果是( ) 【图片】A.5 B.20 C.60 D.120
参考答案:
|
D
|
参考解析:
程序运算的功能是计算
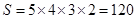 .
.
【简答题】

[5/1010]已知分段函数y= 【图片】,编写伪代码,输入自变量x的值,输出其相应 的函数值,并画出流程图.
参考答案:
参考解析:
伪代码如下:
Read x
If x<0 Then
y ←-x+1
Else
If x="0" Then
y←0
Else
y←x+1
End If
End If
Print y
End 7分
流程图如图所示:
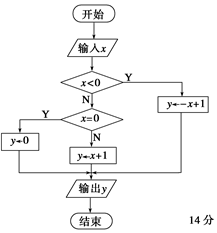
Read x
If x<0 Then
y ←-x+1
Else
If x="0" Then
y←0
Else
y←x+1
End If
End If
Print y
End 7分
流程图如图所示:

【简答题】

[6/1010]有如下算法:第一步,输入不小于2的正整数n 第二步,判断n是否为2,若n=2,则n满足条件;若n>2,则执行第三步第三步,依次从2到n-1检验能...
参考答案:
| A |
参考解析:
无
【简答题】

[7/1010]如图所示,程序框图的功能是( ) 【图片】A.求数列{ 【图片】}的前10项和(n∈N*)B.求数列{ 【图片】}的前10项和(n∈N*)C.求数列...
参考答案:
|
B
|
参考解析:
依题意得,第一次运行,S=
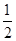 ,n=4,k=2;第二次运行,S=
,n=4,k=2;第二次运行,S=
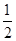 +
+
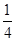 ,n=6,k=3;…;第九次运行,S=
,n=6,k=3;…;第九次运行,S=
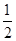 +
+
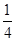 +…+
+…+
 ,n=20,k=10;第十次运行,S=
,n=20,k=10;第十次运行,S=
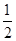 +
+
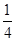 +…+
+…+
 +
+
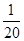 ,n=22,k=11,此时结束循环,故程序框图的功能是求数列{
,n=22,k=11,此时结束循环,故程序框图的功能是求数列{
 }的前10项和.
}的前10项和.
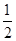 ,n=4,k=2;第二次运行,S=
,n=4,k=2;第二次运行,S=
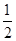 +
+
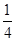 ,n=6,k=3;…;第九次运行,S=
,n=6,k=3;…;第九次运行,S=
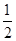 +
+
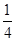 +…+
+…+
 ,n=20,k=10;第十次运行,S=
,n=20,k=10;第十次运行,S=
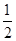 +
+
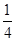 +…+
+…+
 +
+
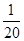 ,n=22,k=11,此时结束循环,故程序框图的功能是求数列{
,n=22,k=11,此时结束循环,故程序框图的功能是求数列{
 }的前10项和.
}的前10项和.
【简答题】

[8/1010]执行右图所示的程序框图,输出的a的值为( ) 【图片】 A. 【图片】 B. 【图片】 C....
参考答案:
|
C
|
参考解析:
根据框图的循环结构,依次
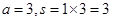 ;
;
 ;
;
 ,此时应跳出循环,输出
,此时应跳出循环,输出
 。故C正确。
。故C正确。
【简答题】

[9/1010]用秦九韶算法求n 次多项式f(x)=anxn+an-1xn-1+…+a1x+a0,当x=x0时,求f(x0)需要算乘方、乘法、加法的次数分别...
参考答案:
| f(x)=anxn+an-1xn-1+…+a1x+a0=(anx^(n-1)+a[n-1]x^(n-2)+…+a[1])x+a[0] =((anxn-2+an-1xn-3+…+a2)x+a1)x+a0 =… =(…((anx+an-1)x+an-2)x+…+a1)x+a0. 求多项式的值时,首先计算最内层括号内一次多项式的值, 即 v1=anx+an-1 然后由内向外逐层计算一次多项式的值,即 v2=v1x+an-2 v3=v2x+an-3… vn=vn-1x+a1 这样,求n次多项式f(x)的值就转化为求n个一次多项式的值. ∴对于一个n次多项式,至多做n次乘法和n次加法 故选D |
参考解析:
无
【简答题】

[10/1010]根据右面的框图,打印的所有数据的和是_____. 【图片】
参考答案:
|
25
|
参考解析:
按照打印顺序依次打印的数为3,7,15,所以其数字和为25.