下载APP

四种命题及其相互关系题库

题数
2000
考试分类
高中数学>四种命题及其相互关系
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-四种命题及其相互关系
...更多
题目预览
【简答题】

[1/2000]已知命题p:a,b,c成等比数列的充要条件是b2=ac;命题q:∀x∈R,x2-x+1>0,则下列结论正确的是( ) A.命题¬p∧q是真命题B.命...
参考答案:
| 因为a,b,c成等比数列所以b2=ac; 反之,若b2=ac,a,b,c不一定成等比数列,例如当a=0,b=0,c=1 所以a,b,c成等比数列是b2=ac的充分不必要条件, 所以命题p是假命题;所以¬p是真命题, 对于x2-x+1,因为△=1-4=-3<0,所以∀x∈R,x2-x+1>0, 所以命题q是真命题; 所以命题¬p∧q是真命题 故选A |
参考解析:
无
【简答题】

[2/2000]已知m∈R,设命题p:关于x的不等式x2+mx+2m<0有解;命题q:若a>b,则am>bm.若命题“¬p”与“p∨q”都为真命题,求m的取值范围.
参考答案:
| ∵命题p:关于x的不等式x2+mx+2m<0有解 ∴若命题p为真命题,则由△=m2-8m>0得, ∴m>8或m<0 ∵命题q:若a>b,则am>bm. ∴命题q为真命题, ∴m>0 ∵“¬p”与“p∨q”都为真命题 ∴命题p为假命题,命题q为真命题 ∴由 |
参考解析:
无
【简答题】

[3/2000]已知命题 【图片】 【图片】,命题 【图片】 【图片】.若命题“ 【图片】”是真命题,求实数 【图片】的取值范围.
参考答案:
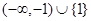 . .
|
参考解析:
求出命题
 成立时的
成立时的
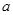 的范围,命题
的范围,命题
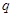 成立时的
成立时的
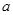 的范围,求出交集即可得到实数
的范围,求出交集即可得到实数
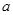 的取值范围.
的取值范围.
命题
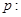 “
“
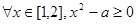 ”,即当
”,即当
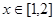 时恒成立,
时恒成立,
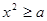 ,
,
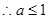 .
.
命题
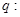 “
“
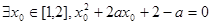 ”, 即方程
”, 即方程
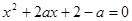 有实根,
有实根,
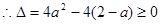 ,
,
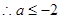 ,或
,或
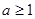 .
.
又
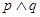 为真命题,故
为真命题,故
 ,
,
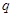 都为真,
都为真,
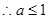 且
且
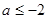 ,或
,或
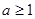 .
.
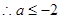 ,或
,或
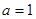 .
.
即实数
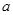 的取值范围为
的取值范围为
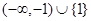 .
.
【简答题】

[4/2000]下列命题: (1)若向量 【图片】,则 【图片】与 【图片】的长度相等且方向相同或相反; (2)对于任意非零向量若 【图片】且 【图片】与 【图片】的...
参考答案:
|
C
|
参考解析:
由于
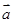 与
与
 可能为零向量,而零向量的方向是任意的,所以(1)若向量
可能为零向量,而零向量的方向是任意的,所以(1)若向量
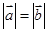 ,则
,则
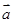 与
与
 的长度相等且方向相同或相反;不正确。
的长度相等且方向相同或相反;不正确。
由相等向量的定义知,(2)对于任意非零向量若
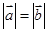 且
且
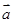 与
与
 的方向相同,则
的方向相同,则
 ;正确。
;正确。
由共线向量的定义知,(3)非零向量
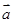 与非零向量
与非零向量
 满足
满足
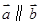 ,则向量
,则向量
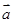 与
与
 方向相同或相反;正确。
方向相同或相反;正确。
向量
 与
与
 是共线向量,意味着两向量方向相同或相反,说
是共线向量,意味着两向量方向相同或相反,说
 四点共线;不正确。
四点共线;不正确。
(5)若
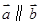 ,且
,且
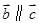 ,则
,则
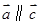 ,不正确,因为,
,不正确,因为,
 为零向量时,不一定
为零向量时,不一定
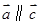 。综上知,选C。
。综上知,选C。
点评:简单题,平面向量的概念较为零碎,学习中应注意加以归纳总结。共线向量是常考点。
【简答题】

[5/2000](满分12分)设命题 P:关于 x的不等式 【图片】的解集为 【图片】;命题Q: 【图片】的定义域为R .如果 P或 Q为真, P且 Q为假,求 【图...
参考答案:
参考解析:
解:P为真时,
 ;Q为真时,
;Q为真时,
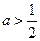 ,因为P或Q为真,P且Q为假, 所以:
,因为P或Q为真,P且Q为假, 所以:
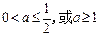
 ;Q为真时,
;Q为真时,
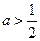 ,因为P或Q为真,P且Q为假, 所以:
,因为P或Q为真,P且Q为假, 所以:
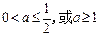
【简答题】

[6/2000]命题“有些大于1 的整数只有两个正因数(1 和它本身)”的否定是 [ ...
参考答案:
| D |
参考解析:
无
【简答题】

[7/2000]有关下列命题,其中说法错误的是 ...
参考答案:
|
C
|
参考解析:
考点:
对于A,命题:“若 ,则
,则
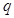 ”逆否命题为“若
”逆否命题为“若
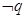 ,则
,则
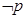 ”,A正确;
”,A正确;
对于B,命题:“若 ,则
,则
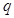 ”逆命题为“若
”逆命题为“若
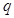 ,则
,则
 ”,B正确;
”,B正确;
对于C,当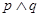 为假命题时,
为假命题时,
 ,
,
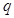 可一真一假,C错误;
可一真一假,C错误;
对于D,命题否定形式只否定原命题的结论.
点评:此题考查逆否命题及逆命题写法,同时考查复合命题.
对于A,命题:“若
 ,则
,则
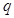 ”逆否命题为“若
”逆否命题为“若
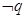 ,则
,则
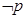 ”,A正确;
”,A正确;
对于B,命题:“若
 ,则
,则
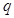 ”逆命题为“若
”逆命题为“若
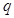 ,则
,则
 ”,B正确;
”,B正确;
对于C,当
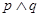 为假命题时,
为假命题时,
 ,
,
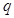 可一真一假,C错误;
可一真一假,C错误;
对于D,命题否定形式只否定原命题的结论.
点评:此题考查逆否命题及逆命题写法,同时考查复合命题.
【简答题】

[8/2000]已知、、为互不重合的三个平面,命题若,,则;命题若上不共线的三点到的距离相等,则。对以上两个命题,下列结论中正确的是 A.命题“且”为真B.命题“或”...
参考答案:
|
C
|
参考解析:
无
【简答题】

[9/2000]命题“若 【图片】”的逆否命题是 ...
参考答案:
|
C
|
参考解析:
无
【简答题】

[10/2000]命题“ 【图片】, 【图片】”的否定是
参考答案:
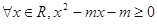
|
参考解析:
主要考察的是命题的否定,对存在命题其否定是所有,故可得