B

解：（I）根据表中所给的数据，写出对应的点的坐标，画出对应的散点图   （II）做出． ∵， ∴样本中心点是（109，23.2） 把样本中心点代入线性回归方程得到． （III）由（II）知，回归直线方程为． 所以，当x=120m2时，销售价格的估计值为=0.196×120+1.836=25.356（万元） 120m2的房屋销售价格估计为25.356万元．

③

（1）设抽到不相邻的两组数据为事件A， 从5组数据中选取2组数 据共有10种情况：（1，2） （1，3）（1，4）（1，5）（2，3）（2，4）（2，5） （3，4）（3，5）（4，5）， 其中数据为12月份的日期数． 每种情况都是可能出现的，事件A包括的基本事件有6种． ∴P（A）= 6 10 = 3 5 ． ∴选取的2组数据恰好是不相邻2天数据的概率是 3 5 （2）由数据，求得 . x =12， . y =27 ． 由公式，求得b= 5 2 ，a= . y -b . x =-3 ∴y关于x的线性回归方程为 ̂ y = 5 2 x-3． （3）当x=10时， ̂ y = 5 2 ×10-3=22，|22-23|＜2； 同样当x=8时， ̂ y = 5 2 ×8-3=17，|17-16|＜2； ∴该研究所得到的回归方程是可靠的．

610

∵5名儿童的年龄分别是3，4，5，6，7， ∴这5名儿童的平均年龄是 3+4+5+6+7 5 =5， ∵用年龄预报体重的回归方程是 ̂ y =3x+5 ∴这5名儿童的平均体重是 ̂ y =3×5+5 =20kg 故答案为：20．

（1）∵根据所给的数据可以得到 n i=1 xiyi =3×5=66.5-------（2分） . x = 3+4+5+6 4 =4.5-------（3分） . y = 2.5+3+4+4.5 4 =3.5-------（4分） n i=1 xi2 =32+42+52+62=86-------（5分） ∴ ̂ b = 66.5-4×4.5×3.5 86-4×4.52 = 66.5-63 86-81 =0.7 -------（8分） ̂ a = . Y - ̂ b . X =3.5-0.7×4.5=0.35 -------（10分） 故线性回归方程为y=0.7x+0.35-------（11分） （2）当x=10（年）时，维修费用是 0.7×10+0.35=7.35 （万元）-------13分 所以根据回归方程的预测，使用年限为10年时，预报维修费用是7.35 （万元）-------14分

n i=1

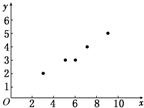（1）依题意，画出散点图如图所示， （2）从散点图可以看出，这些点大致在一条直线附近， 设所求的线性回归方程为 y = b . x + a ． . x = 3+5+6+7+9 5 =6 . y = 2+3+3+4+5 5 =3.4 则 b = 5 i=1  (xi- . x )(yi- . y ) 5 i=1  (xi- . x )2 = 10 20 =0.5， a = . y - b . x =0.4 ， ∴年推销金额y关于工作年限x的线性回归方程为 y =0.5x+0.4． （3）由（2）可知，当x=11时， y =0.5x+0.4=0.5×11+0.4=5.9（万元）． ∴可以估计第6名推销员的年推销金额为5.9万元．

y

（1）因为r≈0.94∈[0.75，1]，所以y与x具有较强的正相关， （2）因为线性回归直线过样本中心点， . x = 70+75+80+85+90 5 =80 ， . y = 73+77+80+88+86 5 =80.8 所以该方程所表示的直线一定经过定点（80，80.8）．

.x

由散点图可知点的分布都集中在一条直线附近，所以由此可以判断两个变量具有相关关系，而且是正相关，所以①正确． 由散点图可知具有相关关系的点的分布都集中在一条直线附近，所以散点图表明两变量具有线性相关关系，所以②正确． 散点图只能体现点的集中程度，并不能说明根据人体脂肪含量和年龄关系的数据所求出的回归方程的图形上，所以③错误． 故答案为：①②．

D