
下载APP

集合的含义及表示题库

题数
1706
考试分类
高中数学>集合的含义及表示
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-集合的含义及表示
...更多
题目预览
【简答题】

[1/1706]已知数集M={x2,1},则实数x的取值范围为______.
参考答案:
| ∵数集M={x2,1}, 根据集合的元素的互异性知x2≠1, ∴x≠±1, ∴实数x的取值范围为{x|x∈R,且x≠±1}, 故答案为:{x|x∈R,且x≠±1} |
参考解析:
无
【简答题】

[2/1706]下列所给关系正确的个数是( )①π∈R;②3∉Q;③0∈N*;④|-4|∉N*. A.1B.2C.3D.4
参考答案:
由于①π∈R;②
③0∉N*;④|-4|∈N*.故①②正确,③④错误 故答案为 B |
参考解析:
3
【简答题】

[3/1706]已知互异的复数a,b满足ab≠0,集合{a,b}={ 【图片】, 【图片】},则 【图片】= &nbs...
参考答案:
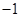
|
参考解析:
由题意
 或
或
 ,因为
,因为
 ,
,
 ,
,
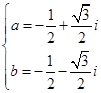
 ,因此
,因此
 .
.
【考点】集合的相等,解复数方程.
 或
或
 ,因为
,因为
 ,
,
 ,
,
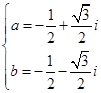
 ,因此
,因此
 .
.
【考点】集合的相等,解复数方程.
【简答题】

[4/1706]若集合M={0,1,2},N={(x,y)|x-2y+1≥0且x-2y-1≤0,x,y∈M},则N中元素的个数为( ) A.9B.6C.4D.2
参考答案:
| 画出集合N所表示的可行域,知满足条件的N中的点只有(0,0)、(1,0)、(1,1)和(2,1)四点, 故选C |
参考解析:
无
【简答题】

[5/1706]已知集合A={x|ax 2-3x+2=0,a∈R}. (1) 若A是空集,求a的取值范围; (2) 若A中只有一个元素,求a的值,并将这个元素写出来;...
参考答案:
|
(1)
 (2) (2)
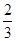 (3)a≥ (3)a≥
 或a=0. 或a=0.
|
参考解析:
(1)若A是空集,则Δ=9-8a<0,解得a>
 .
.
(2) 若A中只有一个元素,则Δ=9-8a=0或a=0,解得a= 或a=0;当a=
或a=0;当a=
 时这个元素是
时这个元素是
 ;当a=0时,这个元素是
;当a=0时,这个元素是
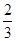 .
.
(3) 由(1)(2)知,当A中至多有一个元素时,a的取值范围是a≥ 或a=0.
或a=0.
 .
.
(2) 若A中只有一个元素,则Δ=9-8a=0或a=0,解得a=
 或a=0;当a=
或a=0;当a=
 时这个元素是
时这个元素是
 ;当a=0时,这个元素是
;当a=0时,这个元素是
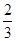 .
.
(3) 由(1)(2)知,当A中至多有一个元素时,a的取值范围是a≥
 或a=0.
或a=0.
【简答题】

[6/1706]下列各项中,能组成集合的是( ) A.高一(3)班的好学生B.嘉兴市所有的老人C.不等于0的实数D.我国著名的数学家
参考答案:
| ∵对于A、B、D“高一(3)班的好学生”、“嘉兴市所有的老人”、“我国著名的数学家”标准不明确,即元素不确定. ∴A、B、D不能构成集合. 故选C |
参考解析:
无
【简答题】

[7/1706]给出下列命题(1)集合{0}不是空集.(2)直线a平面∥α,α∥β,则直线a∥β;(3)二次函数y=1-a(x-1)2有最大值,则 a≤0(...
参考答案:
| 对于(1),集合{0}中含一个元素0,所以(1)对; 对于(2),当直线a平面∥α,α∥β,则直线a∥β或a⊂β,所以(2)错; 对于(3),二次函数y=1-a(x-1)2有最大值,其图象开口向下,所以a>0,所以(3)错; 对于(4),2x-y+5=0的斜率为2,x+3y-1=0的斜率为-
所以(4)对. 故选A. |
参考解析:
13
【简答题】

[8/1706]若x∈A,则1x∈A,就称A是伙伴关系集合,集合M={-1,0, 13, 12,1,2,3,4}的所有非空子集中,具有伙伴关系集合的个数为______...
参考答案:
∵由
∴有24个集合 ∵集合为非空集合,∴有24-1个 故答案为:15 |
参考解析:
13
【简答题】

[9/1706](本小题满分12分)若a,b 【图片】R,集合 【图片】求b-a的值.
参考答案:
|
b-a=2.
|
参考解析:
解 由
 可知a≠0,则只能a+b=0,----------------2分
可知a≠0,则只能a+b=0,----------------2分
则有以下对应关系:
 ①或
①或
 ②----------------------6分
②----------------------6分
由①得 符合题意;-------------------10分
符合题意;-------------------10分
②无解.所以b-a="2.---------------------" 12分
 可知a≠0,则只能a+b=0,----------------2分
可知a≠0,则只能a+b=0,----------------2分
则有以下对应关系:
 ①或
①或
 ②----------------------6分
②----------------------6分
由①得
 符合题意;-------------------10分
符合题意;-------------------10分
②无解.所以b-a="2.---------------------" 12分
【简答题】

[10/1706]设P,Q为两个非空集合,定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6},则P+Q中元素的个数是 [ &...
参考答案:
| B |
参考解析:
无