
下载APP

动量守恒定律的应用题库

题数
254
考试分类
高中物理>动量守恒定律的应用
售价
¥20
收藏
分享
去刷题



章节目录
简介
高中物理-动量守恒定律的应用
...更多
题目预览
【简答题】

[1/254](选修3-5选做题)一质量为M的长木板静止在光滑水平桌面上。一质量为m的小滑块以水平速度v0从长木板的一端开始在木板上滑动,直到离开木板。滑块刚离开木...
参考答案:
解:mv0=m +Mu,u= +Mu,u=  = =  联立解得v=  |
参考解析:
无
【简答题】

[2/254]【选修3-5选做题】如图所示,平放在水平面上的轻质弹簧的一端固定在竖直墙上,质量为m1的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接。一个质量为...
参考答案:
解:设弧形槽与小球第一次分离后的速度大小分别为 和 和 弧形槽和小球在水平方向满足动量守恒  小球与弹簧发生作用后以原速率返回,要使小球和弧形槽发生第二次作用则满足  所以弧形槽和小球的质量应满足  |
参考解析:
无
【简答题】

[3/254](选做题,选修3-5)如图所示,在平静的水面上有A、B两艘小船,A船的左侧是岸,在B 船上站着一个人,人与B船的总质量是A船的10倍。两船开始时都处于...
参考答案:
| 解: 取向右为正,B船上的人第一次推出A船时,由动量守恒定律得mBv1-mAv=0 当A船向右返回后,B船上的人将A接住,有mAv+mBv1=(mA+mB)v2 解得:  。 。 |
参考解析:
无
【简答题】

[4/254]如图所示,两块带有等量异号电荷的平行金属板分别固定在长L=1 m的绝缘板的两端,组成一带电框架,框架右端带负电的金属板上固定一根原长为l0=0.5 m...
参考答案:
|
解:(1)当弹簧刚好恢复原长时小球与弹簧分离,设此时小球的速度为v1,框架的速度为v2,根据动量守恒和能量守恒可列出下列方程: |
参考解析:
无
【简答题】

[5/254]如图所示,凹槽的水平底面宽度s=0.3m,左侧高度H=0.45m,右侧高度h=0.25m。凹槽的左侧竖直面与半径R=0.2m的1/4光滑圆弧轨道相接,...
参考答案:
|
解:(1)P1从A点滑至B点过程中,根据动能定理有: |
参考解析:
无
【简答题】

[6/254]如图所示,木块A静置于光滑的水平面上,其曲面部分MN光滑、水平部分NP粗糙,现有一物体B自M点由静止下滑,设NP足够长,则以下叙述正确的是 【图片】 ...
参考答案:
| BC |
参考解析:
无
【简答题】

[7/254]如图所示,A、B两物体彼此接触静止于光滑的水平桌面上,物体A的上表面是半径为R的光滑圆形轨道,物体C由静止开始从A上圆形轨道的右侧最高点下滑,则有&n...
参考答案:
| BC |
参考解析:
无
【简答题】

[8/254]如图所示,在光滑的水平面上停放着一辆质量为M的小车,小车上的平台是粗糙的,停在光滑的水平桌面旁。现有一质量为m的质点C以初速度v0沿水平桌面向右运动,...
参考答案:
解:(1)设质点C离开平台时的速度为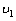 ,小车的速度为 ,小车的速度为 ,对于质点C和小车组成的系统,动量守恒:m ,对于质点C和小车组成的系统,动量守恒:m =m =m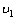 +M +M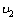 ① ①从质点C离开A后到还未落在小车上以前,质点C作平抛运动,小车作匀速运动,则:  ②, ②, ③ ③由①、②、③式解得: 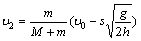 (2)设小车最后运动的速度为 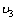 ,在水平方向上运用动量守恒定律:m ,在水平方向上运用动量守恒定律:m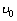 =(M+m) =(M+m)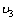 ④ ④设OB水平面的重力势能为零,由能量守恒定律得  ⑤ ⑤由④、⑤两式解得 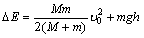 |
参考解析:
无
【简答题】

[9/254]不定项选择 质量均为m的A、B两船静止在湖面上,设水对船的阻力不计,今A船上有一质量为m/2的人以水平速度v从A船跳到B船上,则A、B两船的速度大小之...
参考答案:
| B |
参考解析:
无
【简答题】

[10/254]【选修3-5选做题】质量为M=2 kg的木板若固定在光滑的水平地面上,质量为m=0.04kg的子弹以速度v1=500 m/s射入,射出时子弹速度v2=...
参考答案:
解:木块固定时,系统摩擦力所做的功Wf 将固定木块的钉子拔出后,子弹仍能射出木块。以m和M组成的系统为研究对象,系统在水平方向动量守恒,根据动量守恒和能量守恒得 mv1=mv'+Mv ②  由①②③解得v'= 298.5 m/s |
参考解析:
无




 =2m/s
=2m/s

 解得小球P1从C点抛出时的速度
解得小球P1从C点抛出时的速度 =1.5m/s
=1.5m/s




 时,
时,


 ,解得
,解得
 时,
时,
 时,P2落在右侧竖直面上,故
时,P2落在右侧竖直面上,故 。
。