
下载APP

一元二次不等式及其解法题库

题数
1676
考试分类
高中数学>一元二次不等式及其解法
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-一元二次不等式及其解法
...更多
题目预览
【简答题】

[1/1676]若 【图片】, 【图片】,则 【图片】、 【图片】、 【图片】、 【图片】由小到大的顺序是_____________(用“ 【图片】”连接).
参考答案:

|
参考解析:
无
【简答题】

[2/1676](12分)已知 【图片】(I)当 【图片】时,解不等式 【图片】; (II)若 【图片】,解关于 x的不等式 【图片】。
参考答案:
|
(I)不等式的解为:

(II)当 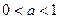 时,有 时,有
 ,∴不等式的解集为 ,∴不等式的解集为
 ; ;
当  时,有 时,有
 ,∴不等式的解集为 ,∴不等式的解集为
 ; ;
当  时,不等式的解为 时,不等式的解为
 。 。
|
参考解析:
解:(I)当
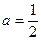 时,有不等式
时,有不等式
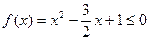 ,
,
∴ ,
,
∴不等式的解为:
(II)∵不等式
当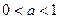 时,有
时,有
 ,∴不等式的解集为
,∴不等式的解集为
 ;
;
当 时,有
时,有
 ,∴不等式的解集为
,∴不等式的解集为
 ;
;
当 时,不等式的解为
时,不等式的解为
 。
。
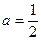 时,有不等式
时,有不等式
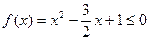 ,
,
∴
 ,
,
∴不等式的解为:

(II)∵不等式

当
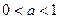 时,有
时,有
 ,∴不等式的解集为
,∴不等式的解集为
 ;
;
当
 时,有
时,有
 ,∴不等式的解集为
,∴不等式的解集为
 ;
;
当
 时,不等式的解为
时,不等式的解为
 。
。
【简答题】

[3/1676]设函数 【图片】的定义域为集合M,函数 【图片】的定义域 为集合N,则 【图片】= &nb...
参考答案:

|
参考解析:
∵
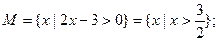
 ,
,
∴ =
=
 .
.
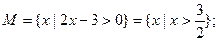
 ,
,
∴
 =
=
 .
.
【简答题】

[4/1676]已知三个不等式:①x2-4x+3<0;②x2-6x+8>0;③2x2-8x+m≤0.要使同时满足①式和②式的所有x的值都满足③式,则实数m的取值范围是...
参考答案:
由
若同时满足①式和②式的所有x的值都满足③式, 说明不等式2x2-8x+m≤0对于x∈(1,2)上恒成立, 即
故选C. |
参考解析:
| x2-4x+3<0 |
| x2-6x+8>0 |
【简答题】

[5/1676]已知 【图片】(1)解关于 【图片】的不等式 【图片】 【图片】(2)若不等式 【图片】的解集为 【图片】求实数 【图片】的值 .
参考答案:
|
解:(1)由已知

(2) 
|
参考解析:
略
【简答题】

[6/1676]若命题“ 【图片】x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为( )
参考答案:
| ﹣1≤a≤3 |
参考解析:
无
【简答题】

[7/1676]解下列关于x的不等式:(1)x2-5x+6>0(2)(x+a)(x-2a+1)<0.
参考答案:
| (1)∵x2-5x+6>0 ∴(x-2)(x-3)>0 ∴x>3或x<2 ∴不等式的解集是{x|x>3或x<2}….(6分) (2)(x+a)(x-2a+1)=0⇒x1=-a,x2=2a-1 ①当-a=2a-1⇒a=
②当-a>2a-1⇒a<
③当-a<2a-1⇒a>
综上所述:当a=
当a<
当a>
|
参考解析:
13
【简答题】

[8/1676]解关于x的不等式 【图片】-( 【图片】+ 【图片】) 【图片】+ 【图片】>0(其中 【图片】∈R).
参考答案:
|
当
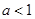 时,解集为 时,解集为
 ;当 ;当
 时,解集为 时,解集为
 ; ;
当  时,解集为 时,解集为
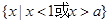 . .
|
参考解析:
解题思路:将
 分解因式得
分解因式得
 ,再讨论1与
,再讨论1与
 的大小求解集.
的大小求解集.
规律总结:解一元二次不等式,要注意“三个二次”的关系,即一元二次方程、一元二次函数、一元二次不等式之间的关系.
注意点:解题中要注意讨论1与
 的大小.
的大小.
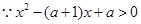 ,
,

则当
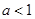 时,解集为
时,解集为
 ;
;
当
 时,解集为
时,解集为
 ;
;
当
 时,解集为
时,解集为
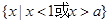 .
.
【简答题】

[9/1676]不等式2x2-x<0的解集为______.
参考答案:
| 由2x2-x<0,得x(2x-1)<0. 即对应方程x(2x-1)=0的两个根分别为x=0或x=
所以不等式2x2-x<0的解为0<x<
故答案为:{x|0<x<
|
参考解析:
无
【简答题】

[10/1676]已知关于x的不等式a(x+1)x-2<2的解集为A,且5∉A,(1)求实数a的取值范围;(2)求集合A.
参考答案:
(1)由题意关于x的不等式
可得
即实数a的取值范围是a≥1 (2)
由(1)知a≥1 当1≤a<2时,不等式可变为
当a=2时,不等式可变为
当a>2时,不等式可变为
综上,当1≤a<2时不等式的解是x>
|
参考解析:
无