
下载APP

等差数列的通项公式题库

题数
1225
考试分类
高中数学>等差数列的通项公式
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-等差数列的通项公式
...更多
题目预览
【简答题】

[1/1225]已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n项和为Sn.(Ⅰ)求an及Sn;(Ⅱ)令 【图片】(n∈N+),求数列{bn}的前...
参考答案:
| 解:(Ⅰ)设等差数列{an}的公差为d, ∵a3=7,a5+a7=26, ∴有  ,解得a1=3,d=2, ,解得a1=3,d=2,∴an=3+2(n﹣1)=2n+1; Sn= 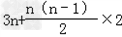 =n2+2n; =n2+2n;(Ⅱ)由(Ⅰ)知an=2n+1, ∴bn= 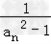 = =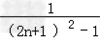 = = = =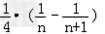 , ,∴Tn= 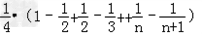 = = = =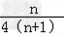 , ,即数列{bn}的前n项和Tn= 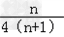 . . |
参考解析:
无
【简答题】

[2/1225]设数列{an}的前n项和为Sn,a1=1,且对任意正整数n,点(an+1,Sn)在直线2x+y-2=0上.(1)求数列{an}的通项公式;(2)若bn...
参考答案:
| (1):(Ⅰ)∵点(an+1,Sn)在直线2x+y-2=0上, ∴2an+1 +Sn -2=0. ① 当n≥2时,2an+sn-1-2=0. ② ①─②得 2an+1 -2an+an=0,即
把n=1和a1=1代入①,可得a2=
∴{an}是首项为1,公比为
则an=(
(2)设数列{bn}的前n项和是Tn, 由(1)得,bn=nan2=n(
∴Tn=1+2×
则
①-②得,
=
则Tn=1-
|
参考解析:
an+1
an
【简答题】

[3/1225]在等比数列{an}中,a2-a1=2,且2a2为3a1和a3的等差中项,求数列{an}的首项、公比及前n项和.
参考答案:
| 设等比数列的公比为q, 由已知可得,a1q-a1=2,4a1q=3a1+a1q2 联立可得,a1(q-1)=2,q2-4q+3=0 ∴
∴sn=
|
参考解析:
无
【简答题】

[4/1225]已知等差数列{an}满足a2=2,a5=8.(1)求{an}的通项公式;(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4,求{bn}...
参考答案:
| (1)设等差数列{an}的公差为d ∵a2=2,a5=8 ∴a1+d=2,a1+4d=8解得 a1=0,d=2 ∴数列{an}的通项公式an=a1+(n-1)d=2n-2 (2)设各项均为正数的等比数列{bn}的公比为q(q>0) 由(1)知an=2n-2 b1=1,b2+b3=a4=6 ∴q≠1 ∴q=2或q=-3(舍去) ∴{bn}的前n项和Tn=2n-1 |
参考解析:
无
【简答题】

[5/1225]已知{an}为等差数列,且a3=-6,a6=0.(1)求{an}的通项公式;(2)求{an}的前n项和.
参考答案:
(1)∵d=
∴an=a3+(n-3)d=2n-12. (2)Sn=
|
参考解析:
a6-
a36-3
【简答题】

[6/1225]已知数列{an}是等差数列,且a1=2,a1+a2+a3=12.(1)求数列{an}的通项公式;(2)若从{an}中依次取出第2项,第4项,第8项,…...
参考答案:
| (1)因为数列{an}是等差数列, 由a1+a2+a3=12可得3a2=12,即a2=4, 又a1=2,∴公差d=a2-a1=4-2=2, 所以数列{an}的通项公式为:an=2n …(4分) (2)由(1)可得bn=a2n=2×2n=2n+1…(6分) 当n≥2时,
所以数列{bn}是首项为4,公比为2的等比数列 …(8分) |
参考解析:
bn
bn-1
【简答题】

[7/1225]若等差数列{an}的前5项和Sn=25,且a2=3,则a4=______.
参考答案:
| ∵等差数列{an}的前5项和Sn=25,且a2=3, ∴
∴a3=5,d=a3-a2=5-3=2, ∴a4=a3+d=5+2=7. 故答案为:7. |
参考解析:
|
||
| a2=3 |
【简答题】

[8/1225]已知公差不为零的等差数列{an}中,M=an·an+3,N=an+1·an+2,则M与N的大小关系是( )。
参考答案:
| M<N |
参考解析:
无
【简答题】

[9/1225]已知y=f(x)定义在R上的单调函数,当x<0时,f(x)>1,且对任意的实数x、y∈R,有f(x+y)=f(x)·f(y),设数列{an}满足a1=...
参考答案:
| 解:(Ⅰ)由题意,令y=0,x<0,得f(x)[1﹣f(0)]=0, ∵当x<0时,f(x)>1,∴a1=f(0)=1 由递推关系知f(an+1)?f(﹣2﹣an)=1,即f(an+1﹣2﹣an)=f(0), ∵f(x)在R上单调,∴an+1﹣an=2,(n∈N*), 又a1=1,∴an=2n﹣1. (Ⅱ) 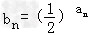 = =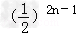 , ,∴ 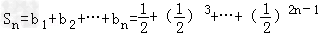 = =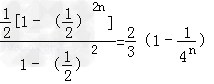 , ,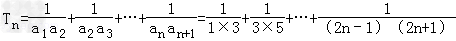 = 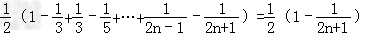 , , , ,∴欲比较Sn与 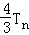 的大小,只需比较4n与2n+1的大小. 的大小,只需比较4n与2n+1的大小.∵4n=(1+3)n=Cn0+Cn1?3+…+Cnn?3n≥1+3n>2n+1, ∴Sn>  . . |
参考解析:
无
【简答题】

[10/1225]已知数列{an}的前n项和Sn=2n2,则an=______.
参考答案:
| 当n=1时,S1=2×12=2, 当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2, 又n=1时,a1=2,满足通项公式, ∴此数列为等差数列,其通项公式为an=4n-2, 故答案为:4n-2. |
参考解析:
无