二面角题库 - 考试题库

【简答题】

[1/438]如图，矩形ABCD中，AB=a，AD=b，过点D作DE⊥AC于E，交直线AB于F．现将△ACD沿对角线AC折起到△PAC的位置，使二面角P-AC-B的...

参考答案：

（I）证明：∵AC⊥PE，AC⊥EF，又PE∩EF=E，∴AC⊥平面PEF，
∵AC⊂平面ABC，∴平面PEF⊥平面ABC，
∵平面PEF∩平面ABC=EF，PH⊥EF，PH⊂平面PEF，
∴PH⊥平面ABC．
（II）∵PE⊥AC，EF⊥AC
∴∠PEF为二面角P-AC-B的平面角，∴∠PEF=60°
∴EH=

1

2

PE=

1

2

DE ，PH=

参考解析：

无

【简答题】

[2/438]如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．（1）证明：AC⊥PB；（2）证明：P...

参考答案：

（1）证明：∵PA⊥平面ABCD，AC在平面ABCD内，∴AC⊥PA
又AC⊥AB，PA∩AB=A，∴AC⊥平面PAB（2分）
又PB在平面PAB内，∴AC⊥PB（4分）
（2）证明：连结BD，与AC相交于O，连结EO
∵ABCD是平行四边形，∴O是BD的中点（5分）
又E为PD中点，∴PB∥EO（6分）
又PB在平面AEC外，EO在AEC平面内，∴PB∥平面AEC（8分）
（3）过O作FG∥AB，交AD于F，交BC于G，则F为AD中点
∵AB⊥AC，∴OG⊥AC
又由（1）（2）知，AC⊥PB，EO∥PB，
∴AC⊥EO（10分）
∴∠EOG是二面角E-AC-B的平面角
连结EF，在△EFO中，FO=

1

2

AB
又PA=AB，EF⊥FO，∴∠EOF=45°
∴∠EOG=135°，即二面角E-AC-B的大小为135°．（12分）

参考解析：

12

【简答题】

[3/438]已知边长为m的正方形ABCj沿对角线AC折成直二面角，使j到P的位置．（四）求直线PA与BC所成的角；（m）若M为线段BC上的动点，当BM：BC为何值...

参考答案：

（1）取AC四点O，连接PO、OB，以O为原点建立如图所示的空间直角坐标系，
则P（0，0，1），A（（0，-1，0），B（1，0，0），C（0，1，0），

参考解析：

【简答题】

[4/438]正三棱锥的相邻两侧面所成的角为α，则α的取值范围（　　） A．（【图片】，π） B．（【图片】，π） C．（【图片】，【图片】） D．（【图...

参考答案：

B

参考解析：

无

【简答题】

[5/438]如图，在直三棱柱ABC-A1B1C1中，AB=4，AC=BC=3，D为AB的中点。【图片】（1）求点C到平面A1ABB1的距离；（2）若AB1⊥A...

参考答案：

解：（1）由AC=BC，D为AB的中点，得CD⊥AB
又CD⊥AA₁。
故CD⊥平面A₁ABB₁．
所以点C到平面A₁ABB₁的距离为CD=

。

（2）如图，取D₁为A₁B₁的中点，连接DD₁，则DD₁∥AA₁∥CC₁又由（1）知CD⊥平面A₁ABB₁故CD⊥A₁D，CD⊥D₁D，
所以∠A₁DD₁为所求的二面角A₁-CD-C₁的平面角
因A₁D为A₁C在面A₁ABB₁中的射影，
又已知AB₁⊥A₁C由三垂线定理的逆定理得AB₁⊥A₁D
从而∠A₁AB₁、∠A₁DA都与∠B₁AB互余
因此∠A₁AB₁=∠A₁DA，
所以Rt△A₁AD∽Rt△B₁A₁A
因此AA₁：AD=A₁B₁：AA₁，即AA₁²=AD?A₁B₁=8，得AA₁=2 ，
从而A₁D=

所以Rt△A₁D₁D中，cos∠A₁DD₁=

参考解析：

无

【简答题】

[6/438]在棱长为a的正方体ABCD-A1B1C1D1中，E、F分别为棱AB和BC的中点，EF与BD交于点G．（1）求二面角B1-EF-B的正切值；（2）M为棱...

参考答案：

（1）在底面ABCD中，∵AC⊥BD，EF∥AC，∴BG⊥EF，连接B₁G．
又∵BB₁⊥ABCD，∴B₁G⊥EF．
则∠B₁GB是二面角B₁-EF-B的平面角，BG=

1

4

BD=

2

4

a，
tan∠B1GB=

B1B

BG

=2

2

．
（2）当

B1M

MB

=1 时满足题意．
证明：D₁A₁⊥面AB₁，知D₁M在面AB₁的射影是A₁M，
∵△A₁MB≌△B₁EB，∴A₁M⊥B₁E，即D₁M⊥B₁E．
因为DD₁⊥平面ABCD，所以BD为D₁M在平面ABCD内射影，
连接AC，因为E、F为中点，所以AC∥EF，
又因为BD⊥EF，所以D₁M⊥EF．又因为B₁E∩EF=E．
∴D₁M⊥平面EFB₁

参考解析：

14

【简答题】

[7/438]如图1，已知ABCD是上、下底边长分别为2和6，高为【图片】的等腰梯形，将它沿对称轴OO1折成直二面角，如图2。【图片】【图片】（...

参考答案：

解：（1）由题设知OA⊥OO₁，OB⊥OO₁，所以∠AOB是所折成的直二面角的平面角，即OA⊥OB 从而AO⊥平面OBCO₁， OC是AC在面OBCO₁内的射影因为，所以∠OO₁B=60°，∠O₁OC=30°，从而OC⊥BO₁ 由三垂线定理得AC⊥BO₁。
（2）由（1）AC⊥BO₁，OC⊥BO₁，知BO₁⊥平面AOC 设OC∩O₁B=E，过点E作EF⊥AC于F，连结O₁F（如图），则EF是O₁F在平面AOC 内的射影，由三垂线定理得O₁F⊥AC 所以∠O₁FE是二面角O-AC-O₁的平面角由题设知OA=3，OO₁=，O₁C=1，所以从而又O₁E=OO₁·sin30°=，所以即二面角O-AC-O₁的大小是。

参考解析：

无

【简答题】

[8/438]已知正三棱柱ABC-A1B1C1的每条棱长均为a，M为棱A1C1上的动点．（1）当M在何处时，BC1∥平面MB1A，并证明之；（2）在（1）下，求平面...

参考答案：

（I）当M在A₁C₁中点时，BC₁∥平面MB₁A
∵M为A₁C₁中点，延长AM、CC₁，使AM与CC₁延长线交于N，则NC₁=C₁C=a
连接NB₁并延长与CB延长线交于G，则BG=CB，NB₁=B₁G（2分）
在△CGN中，BC₁为中位BC₁∥GN
又GN⊂平面MAB₁，∴BC₁∥平面MAB₁（4分）
（II）∵△AGC中，BC=BA=BG∴∠GAC=90°
即AC⊥AG又AG⊥AA₁AA₁∩AC=A∴AG⊥平面A₁ACC₁，AG⊥AM（6分）
∴∠MAC为平面MB₁A与平面ABC所成二面角的平面角∴tan∠MAC=

a

1

2

a

=2
∴所求二面角为 arctan2．（8分）
（Ⅲ）设动点M到平面A₁ABB₁的距离为h_M．VB-AB1M=VM-AB1B=

1

3

S△ABB1•hM=

1

3

•

1

2

a2hM≤

1

6

a2•

参考解析：

无

【简答题】

[9/438]如图：在直三棱柱ABC-DEF中，AB=2，AC=AD=2 3，AB⊥AC，（1）证明：AB⊥DC，（2）求二面角A-DC-B的余弦值．【图片】

参考答案：

（1）在直三棱柱ABC-DEF中，则AD⊥AB，
又∵AB⊥AC，AD∩AC=A．
∴AB⊥平面ACFD，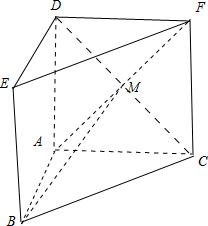

∴AB⊥CD．
（2）由（1）可得：四边形ACFD为正方形，
连接对角线AF、CD相较于点M，则AM⊥CD．
又∵AB⊥平面ACFD，根据三垂线定理可得CD⊥BM．
∴∠AMB是二面角A-DC-B的平面角．
∵AM=

1

2

×2

参考解析：

无

【简答题】

[10/438]如图，在多面体ABCD-A1B1C1D1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E，F两点，上、下底面...

参考答案：

（Ⅰ）解：过B₁C₁作底面ABCD的垂直平面，
交底面于PQ，过B₁作B₁G⊥PQ，垂足为G，
∵平面ABCD∥平面A₁B₁C₁D₁，∠A₁B₁C₁=90°，
∴AB⊥PQ，AB⊥B₁P，
∴∠B₁PG为所求二面角的平面角，
过C₁作C₁H⊥PQ，垂足为H，
由于相对侧面与底面所成二面角的大小相等，
故四边形B₁PQC₁为等腰梯形，
∴

，
又

，
∴

，
即所求二面角的大小为

。
（Ⅱ）证明：∵AB，CD是矩形ABCD的一组对边，
有AB∥CD，
又CD是面ABCD与面CDEF的交线，
∴AB∥面CDEF，
∵EF是面ABFE与面CDEF的交线，
∴AB∥EF，
∵AB是平面ABCD内的一条直线，EF在平面ABCD外，
∴EF∥面ABCD。
（Ⅲ）V_估＜V；
证明：∵a＞c，b＞d，
∴

，
∴V_估＜V。

参考解析：

无