
下载APP

圆的标准方程与一般方程题库

题数
1968
考试分类
高中数学>圆的标准方程与一般方程
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-圆的标准方程与一般方程
...更多
题目预览
【简答题】

[1/1968]已知定点A(2,0),P点在圆x2+y2=1上运动,∠AOP的平分线交PA于Q点,其中O为坐标原点,求Q点的轨迹方程.
参考答案:
| 解:在△AOP中,∵OQ是DAOP的平分线, ∴ 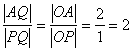 , , 设Q点坐标为(x,y),P点坐标为(x0,y0), ∴ 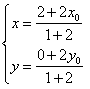 ,即 ,即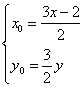 , , ∵ P(x0,y0)在圆x2+y2=1上运动, ∴x02+y02=1,即 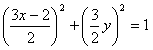 , ,∴ 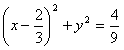 ,此即Q点的轨迹方程。 ,此即Q点的轨迹方程。 |
参考解析:
无
【简答题】

[2/1968](本题满分12分) 在直角坐标系 【图片】中,动点 【图片】到两圆 【图片】的圆心 【图片】和 【图片】的距离的和等于 【图片】. (Ⅰ) 求动点 【...
参考答案:
|
解:(Ⅰ)两圆的圆心坐标分别为
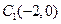 、 、
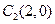 ,根据椭圆的定义可知,动点 ,根据椭圆的定义可知,动点
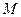 的轨迹为以 的轨迹为以
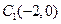 、 、
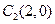 为焦点,长轴长等于 为焦点,长轴长等于
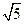 的椭圆. 的椭圆.
由 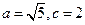 得 得
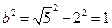 ,所以,动点 ,所以,动点
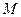 的轨迹方程 的轨迹方程
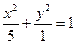
(Ⅱ)由(Ⅰ)得C点的坐标为 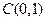
不妨设A、B两点分居于y轴的左、右两侧,设CA的斜率为 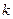 , ,
则 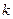 >0,CA所在直线的方程为 >0,CA所在直线的方程为
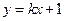 . .
代入椭圆方程并整理得  . .
∴ 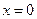 或 或
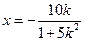 .∴A点的坐标为 .∴A点的坐标为
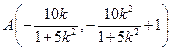 . .
∴ 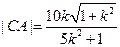 . 同理, . 同理,
 . .
由|CA|=|CB|得 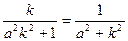 , ,
∴ 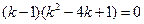 解得 解得
 或 或
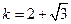 或 或
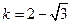
∴符合题意的等腰直角三角形一定存在,且有3个. |
参考解析:
无
【简答题】

[3/1968]直线 【图片】与圆 【图片】( 【图片】)相交于A,B两点,且弦AB的中点为 (0,1),则直线,的方程是( ) ...
参考答案:
|
D
|
参考解析:
无
【简答题】

[4/1968]已知圆 【图片】: 【图片】,过 【图片】轴上的点 【图片】存在圆 【图片】的割线 【图片】,使得 【图片】,则点 【图片】的横坐标 【图片】的取值范...
参考答案:
|
C
|
参考解析:
极端原理,或利用圆幂定理和切长定理
设
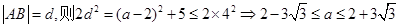 ,故可知点P的横坐标
,故可知点P的横坐标
 的取值范围是
的取值范围是
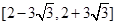 ,选C.
,选C.
点评:解决的关键是利用切线长定理,以及圆内性质的综合运用,属于基础题。
【简答题】

[5/1968]圆心为点 【图片】,且过点 【图片】的圆的标准方程是 ...
参考答案:

|
参考解析:
略
【简答题】

[6/1968]已知圆 【图片】为圆上任意一点,求 【图片】的取值范围( ) A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
A
|
参考解析:
略
【简答题】

[7/1968]点 【图片】在圆 【图片】的( ). A.内部B.外部C.圆上D.与θ的值有关
参考答案:
|
A
|
参考解析:
本题考查圆的参数方程与普通方程的互化及点与圆的位置关系
由 得
得
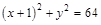
又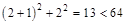
则点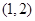 在圆内
在圆内
正确答案为A
由
 得
得
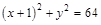
又
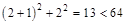
则点
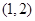 在圆内
在圆内
正确答案为A
【简答题】

[8/1968]圆心为C(1,-2),半径长是3的圆的标准方程是______.
参考答案:
| ∵圆的圆心为C(1,-2),半径长是3, ∴圆的标准方程是(x-1)2+(y+2)2=9 故答案为:(x-1)2+(y+2)2=9 |
参考解析:
无
【简答题】

[9/1968]已知曲线C的参数方程为 【图片】( 【图片】为参数),则曲线C的普通方程是 ;点A在曲线C上,点 【图...
参考答案:
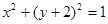
|
参考解析:
:如图,点
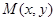 所在的平面区域为阴影部分所示,
所在的平面区域为阴影部分所示,
圆心C到平面区域内点距离的最小值为的线段 的长,
的长,
其中,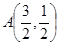 ,
,
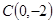 ,圆C的半径
,圆C的半径
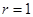 ,
,
故|AM|最小值是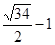 。
。
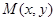 所在的平面区域为阴影部分所示,
所在的平面区域为阴影部分所示,
圆心C到平面区域内点距离的最小值为的线段
 的长,
的长,
其中,
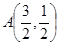 ,
,
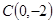 ,圆C的半径
,圆C的半径
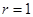 ,
,
故|AM|最小值是
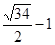 。
。
【简答题】

[10/1968]要使 【图片】与 【图片】轴的两个交点分别位于原点的两侧,则有( ) A. 【图片】B. 【图片】C. 【图片】D....
参考答案:
|
D
|
参考解析:
无