
下载APP

对数函数的图象与性质题库

题数
1965
考试分类
高中数学>对数函数的图象与性质
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-对数函数的图象与性质
...更多
题目预览
【简答题】

[1/1965]设函数f(x)=log2(ax-bx),且f(1)=1,f(2)=log212,(1)求a,b的值;(2)当x∈[1,2]时,求f(x)的最大值。
参考答案:
解:(1)由题设得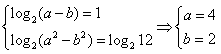 ; ;(2)因为 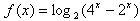 , ,由 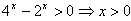 , ,即f(x)的定义域为{x|x>0}, 因为x∈[1,2]为(0,+∞)的真子集, 令 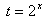 ,则2≤t≤4, ,则2≤t≤4,于是,  , ,又 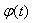 在[2,4]上为增函数, 在[2,4]上为增函数,所以f(x)的最大值为  。 。 |
参考解析:
无
【简答题】

[2/1965]若a2=3,且a>0,则log3a的值为( ) A.- 3B.3C.- 12D.12
参考答案:
由a2=3,且a>0,得:a=3
所以log3a=log33
故选D. |
参考解析:
无
【简答题】

[3/1965]若函数 【图片】在[2,+∞)是增函数,则实数a的取值范围为( )。
参考答案:
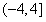 |
参考解析:
无
【简答题】

[4/1965]若f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1)。(1)求f(log2x)的最小值及对应的x值;(2)x取何值时,...
参考答案:
|
解:(1)∵f(x)=x2-x+b, |
参考解析:
无
【简答题】

[5/1965]设f(x)= 11+2lgx+ 11+4lgx+ 11+8lgx,则f(x)+f( 1x)=( ) A.1B.2C.3D.4
参考答案:
∵f(x)=
∴f(x)+f(
=(
=
=3 故选C |
参考解析:
11+
2lgx
【简答题】

[6/1965]对于函数y=|lgx|,若存在0<a<b,且f(a)=f(b),则a+b的取值范围为______.
参考答案:
| 由f(a)=f(b)且0<a<b可得f(a)<0,f(b)>0.且-lg(a)=lg(b) ∴lgab=0 ∴ab=1 由0<a<b可得0<a<1<b (法一):由基本不等式可得,a+b>2
(法二):∵a+b=a+
∴a+
∴a+b>2 故答案为:(2,+∞) |
参考解析:
ab
【简答题】

[7/1965]设5lgx=25,则x的值等于( ) A.10 B.0.01 C.100 D.1000
参考答案:
| C |
参考解析:
无
【简答题】

[8/1965]已知幂函数y=f(x)的图象过点(- 12,- 18),则log2f(4)的值为( ) A.3B.4C.6D.-6
参考答案:
由幂函数y=f(x)的图象过点(-
得(-
则f(x)=x3,f(4)=64 目log2f(4)=log264=6 故选C |
参考解析:
12
【简答题】

[9/1965]若lgx+lgy=2,则1x+ 1y的最小值为______.
参考答案:
| 由lgx+lgy=lgxy=2,得到xy=102=100,且x>0,y>0, ∴
则
故答案为:
|
参考解析:
无
【简答题】

[10/1965]lg8+3lg5的值是( ) A.3 B.1 C.-1 D.-3
参考答案:
| A |
参考解析:
无
 )2+
)2+
 ,即x=
,即x= 时,f(log2x)有最小值
时,f(log2x)有最小值 。
。

 。
。