
下载APP

函数的单调性、最值题库

题数
2000
考试分类
高中数学>函数的单调性、最值
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-函数的单调性、最值
...更多
题目预览
【简答题】

[1/2000]设函数f(x)=x2+2 (x≤2)2x (x>2)则f(-4)=______,又...
参考答案:
因为函数f(x)=
又由于知f(x0)=8,若x0∈{x|x≤2}时,令x02+2=8⇒x0=
若x0∈{x|x>2}时,令2x0=8⇒x0=4. 故答案为:4或-
|
参考解析:
无
【简答题】

[2/2000]已知函数f(x)= 3-axa-2 (a≠2),若f(x)在区间(0,1]上是减函数,则实数a的取值范围是______.
参考答案:
∵已知函数f(x)=
①当a>2时,由根式的性质可得应有3-a×1≥0,解得 2<a≤3,满足函数f(x)=
②当a<0时,a-2<0,且当0<x≤1时,3-ax>0,满足函数f(x)=
③当0<a<2时,a-2<0,且当0<x≤1时,3-ax>0,此时函数f(x)=
综合可得,实数a的取值范围是(-∞,0)∪(2,3], 故答案为 (-∞,0)∪(2,3]. |
参考解析:
无
【简答题】

[3/2000]下列四个函数:(1) 【图片】 (2) 【图片】 (3...
参考答案:
|
B
|
参考解析:
①
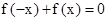 中
中
 ,函数
,函数
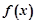 是奇函数②对定义域内的任意两个自变量
是奇函数②对定义域内的任意两个自变量
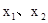 ,都有
,都有
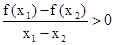 则函数
则函数
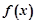 是增函数(1)
是增函数(1)
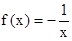 是奇函数,定义域上不是增函数,
是奇函数,定义域上不是增函数,
(2)
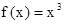 既是奇函数又是增函数(3)
既是奇函数又是增函数(3)
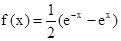 是既是奇函数又是减函数(4)
是既是奇函数又是减函数(4)
 既是奇函数又是增函数。满足题干的有(2) (4)两个
既是奇函数又是增函数。满足题干的有(2) (4)两个
点评:若函数满足
 则函数为奇函数,若满足
则函数为奇函数,若满足
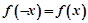 则函数为偶函数,若有
则函数为偶函数,若有
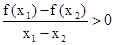 则函数为增函数,若
则函数为增函数,若
 则函数为减函数
则函数为减函数
【简答题】

[4/2000]函数f(x)=(x+a)3,对任意t∈R,总有f(1+t)=-f(1-t),则f(2)+f(-2)=( ) A.0B.2C.-26D.28
参考答案:
| 由f(x)满足对任意t∈R,总有f(1+t)=-f(1-t), 所以函数y=f(x)的图象关于点(1,0)中心对称. 则f(x+1)关于原点中心对称,即g(x)=f(x+1)=(x+1+a)3的图象关于原点中心对称. 所以函数g(x)=(x+1+a)3为奇函数. 所以g(0)=(a+1)3=0. 则a=-1. 所以f(x)=(x-1)3. 则f(2)+f(-2)=(2-1)3+(-2-1)3=-26. 故选C. |
参考解析:
无
【简答题】

[5/2000]已知函数 【图片】满足对任意 【图片】,都有 【图片】 成立,则 【图片】的取值范围为( ) A. 【图片】B.(0,...
参考答案:
|
A
|
参考解析:
因为函数
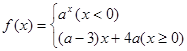 满足对任意
满足对任意
 ,都有
,都有
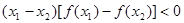 成立,则函数单调递增,因此满足各段递增,同时当x=0时的函数值
成立,则函数单调递增,因此满足各段递增,同时当x=0时的函数值
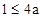 ,这样解得为选项A
,这样解得为选项A
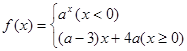 满足对任意
满足对任意
 ,都有
,都有
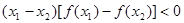 成立,则函数单调递增,因此满足各段递增,同时当x=0时的函数值
成立,则函数单调递增,因此满足各段递增,同时当x=0时的函数值
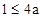 ,这样解得为选项A
,这样解得为选项A
【简答题】

[6/2000]已知函数y=f(x)是R上的偶函数,对于x∈R都有f(x-6)=f(x)+f(3)成立,且f(0)=-2,当x1,x2∈[0,3],且x1≠x2时,都...
参考答案:
| ①②④ |
参考解析:
无
【简答题】

[7/2000]已知f(x)为R上的减函数,则满足 【图片】的实数x的取值范围是 [ ] A.(﹣∞,1) B.(1,...
参考答案:
| D |
参考解析:
无
【简答题】

[8/2000]已知函数f(x)= 2x-log21+mx1-x是奇函数.(1)求m的值;(2)请讨论它的单调性,并给予证明.
参考答案:
| (1)∵f(x)是奇函数,∴f(-x)+f(x)=0; 即(-
经验证当m=1时,f(x)=
(2)先研究f(x)在(0,1)内的单调性,任取x1、x2∈(0,1),且设x1<x2,则 f(x1)-f(x2)=
由
得f(x1)-f(x2)>0,即f(x)在(0,1)内单调递减; 由于f(x)是奇函数,其图象关于原点对称,所以函数f(x)在(-1,0)内单调递减. |
参考解析:
无
【简答题】

[9/2000]求函数 【图片】, 【图片】的单调增区间_________________。
参考答案:
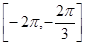 , ,

|
参考解析:
 ,令
,令
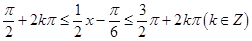
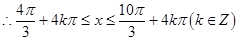 ,当
,当
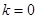 时,
时,
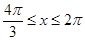 ,当
,当
 时,
时,
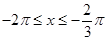
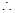 函数的增区间为
函数的增区间为
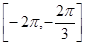 ,
,

点评:求
 的单调区间,先将
的单调区间,先将
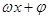 看做一个整体来对待
看做一个整体来对待
【简答题】

[10/2000]已知R上的奇函数f(x)在区间(-∞,0)上单调递增的,且f(-2)=0,则不等式f(x)≤0的解集为 [ &nbs...
参考答案:
| A |
参考解析:
无