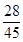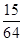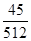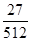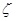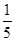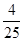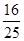下载APP

离散型随机变量及其分布列题库

题数
651
考试分类
高中数学>离散型随机变量及其分布列
售价
¥25
收藏
分享
去刷题



章节目录
简介
高中数学-离散型随机变量及其分布列
...更多
题目预览
【简答题】

[1/651]某学校举办一场以“为希望工程献爱心”为主题的图书义卖活动,同学甲随机地从10本书中买两本,假设每本书被甲同学买走的概率相同,已知这10本书中有3本单价...
参考答案:
| (1)由题意可得:ξ可能取的值为:20,25,30,35,40, 所以P(ξ=2)=
所以随机变量ξ的分布列为:
随机变量ξ的期望Eξ=20×
方差Dξ=(20-30)2×
|
参考解析:
| C | 23 |
| C | 210 |
【简答题】

[2/651]国家对空气质量的分级规定如下表: 污染指数 0~50 51~100 101~150 151~200 201~300 >300 空气质量 优 良 轻度污...
参考答案:
| (I)由某市去年6月份30天的空气污染指数的监测数据表知, a=6,b=3,x=
(Ⅱ)由题意,该市4月份空气质量为优或良的概率为P=
P(X=0)=
∴X的分布列为:
∵X~B(4,
∴EX=4×
|
参考解析:
15
【简答题】

[3/651]已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2只正品,每次取一个,取出后不放回,直到取出2个正品为止.设X为取出的次数,求X的概率分布列...
参考答案:
|
X的概率分布列如下表
|
参考解析:
X
2
3
4
P



2
3
4
P



【简答题】

[4/651]已知随机变量的概率分布如下: 1 2 3 4 5 6 7 8 9 10 P 【图片】 【图片】 【图片】 【图片】 【图片】 【图片】 ...
参考答案:
| C |
参考解析:
无
【简答题】

[5/651]甲、乙两同学进行下棋比赛,约定每局胜者得1分,负者得0分(无平局),比赛进行到有一个人比对方多2分或比满8局时停止,设甲在每局中获胜的概率为 【图片】...
参考答案:
|
(Ⅰ)程序框图中的①应填
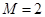 ,②应填 ,②应填
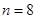 .(注意:答案不唯一.) .(注意:答案不唯一.)
(Ⅱ)依题意得,当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止. 所以 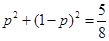 ,解得: ,解得:
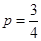 或 或
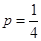 ,因为 ,因为
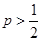 ,所以 ,所以
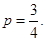
(Ⅲ)依题意得, 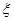 的可能值为2,4,6,8. 的可能值为2,4,6,8.
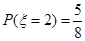 , ,
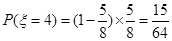 , ,
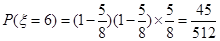 , ,
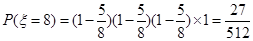 . .
所以随机变量 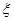 的分布列为 的分布列为
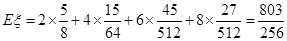
|
参考解析:

2
4
6
8
P




【简答题】

[6/651]某一随机变量 【图片】的概率分布如下表,且 【图片】 【图片】,则 【图片】的值为( ) A.-0.2;B.0.2;C.0.1;D.-0.1 【图...
参考答案:
|
B
|
参考解析:
由离散型随机变量分布列的性质可得。
由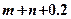
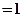 ,又
,又
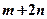
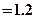 ,可得
,可得
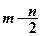
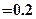
由
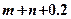
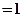 ,又
,又
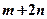
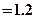 ,可得
,可得
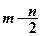
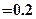
【简答题】

[7/651]某品牌汽车4 【图片】店经销 【图片】三种排量的汽车,其中 【图片】三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买...
参考答案:
|
(1)
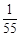 ;(2)详见解析. ;(2)详见解析.
|
参考解析:
(1)这是一个古典概型问题,先求出从15款车型中任买3辆共有多少种可能,再求出购买3辆车都为B种车有多少种可能,即可求出结果;(2)
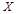 的所有可能取值为1,2,3,对每种情况要准确分类,求出各种情况下有多少种可能,就可求出
的所有可能取值为1,2,3,对每种情况要准确分类,求出各种情况下有多少种可能,就可求出
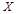 各种取值的概率,然后再求数学期望.
各种取值的概率,然后再求数学期望.
(1)设该单位购买的3辆汽车均为
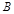 种排量汽车为事件
种排量汽车为事件
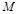 ,则
,则
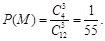
所以该单位购买的3辆汽车均为
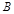 种排量汽车的概率为
种排量汽车的概率为
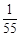 . 4分
. 4分
(2)随机变量
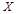 的所有可能取值为1,2,3.
的所有可能取值为1,2,3.
则
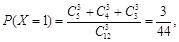
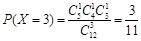 ,
,
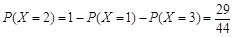 .
.
所以
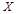 的分布列为
的分布列为
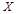 |
1 |
2 |
3 |
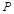 |
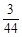 |
 |
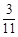 |
数学期望
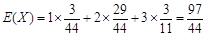 . 10分
. 10分
【简答题】

[8/651]为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素 【图片】, 【图片】的含量(单位:毫...
参考答案:
|
(1)35件(2)分布列如下:
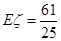
|
参考解析:

1
2
3
P



【简答题】

[9/651]设l为平面上过点(0,1)的直线,l的斜率等可能的取-22,-3,-52,0,52,3,22.用ξ表示坐标原点到l的距离,求随机变量ξ的数学期望E(ξ...
参考答案:
解析 设直线l的方程为y=kx+1.,则原点到直线l的距离d=
当k=0时,d=1;当k=±
所以ξ的分布列为
|
参考解析:
1
| k2+1 |
【简答题】

[10/651]已知离散型随机变量X的分布列如表.若EX=0,DX=1,则a=______,b=______. X -1 0 1 2 P a b c 112
参考答案:
由题知a+b+c=
-a+c+
12×a+12×c+22×
∴a=
故答案为:
|
参考解析:
1112