
下载APP

异面直线所成的角题库

题数
987
考试分类
高中数学>异面直线所成的角
售价
¥25
收藏
分享
去刷题



章节目录
简介
高中数学-异面直线所成的角
...更多
题目预览
【简答题】

[1/987]如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=...
参考答案:
| 解:∵PO⊥平面ABCD, ∴PO⊥BD 又PB⊥PD,BO=2,PO=  , , ∴OD=OC=1,BO=AO=2, 以O为原点,OA、OB、OP分别为x、y、z轴建立如图所示的空间直角坐标系, 则各点坐标为O(0,0,0),A(2,0,0),B(0,2,0),C(-1,0,0),D(0,-1,0),P(0,0,  )。 )。(1)∵  , , ∴  ∴   故直线PD与BC所成角的余弦值为  。 。(2)设平面PAB的一个法向量为n=(x,y,z) 由于  得  令x=1,则y=1,z=  ∴n=(1,1,  ) )又易知平面ABCD的一个法向量m=(0,0,1), ∴cos〈m,n〉=  又二面角P-AB-C是锐角, ∴所求二面角P-AB-C的大小为45°。 (3)设M(x0,0,z0),由于P、M、C三点共线, ∴  ① ①∵PC⊥平面BMD, ∴OM⊥PC ∴(-1,0,-  )·(x0,0,z0)=0 )·(x0,0,z0)=0∴  ② ②由①②知  ∴  ∴  =2 =2故λ=2时,PC⊥平面BMD。 |
 |
参考解析:
无
【简答题】

[2/987]如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的大小是( &...
参考答案:
 |
参考解析:
无
【简答题】

[3/987]若一条直线与一个正四棱柱各个面所成的角都为 【图片】,则 【图片】=_____.
参考答案:
|
60°
|
参考解析:
无
【简答题】

[4/987]空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF= 【图片】,则异面直线AD,BC所成的角为( &nbs...
参考答案:
|
B
|
参考解析:
设G为AC的中点,由已知中AD=BC=2,E、F分别是AB、CD的中点,若EF=

,根据三角形中位线定理,我们易求出∠EGF为异面直线AD、BC所成的角(或其补角),解三角形EGF即可得到答案.
【简答题】

[5/987]如图,在直三棱柱ABC-A1B1C1中,AB=AA1=2,AC=4,∠BAC=90°,D是AB的中点.(Ⅰ)求证:AC1∥平面B1DC;(Ⅱ)求二面角...
参考答案:
 (Ⅰ)证明:如图建立空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,2), B1(2,0,2),C1(0,4,2),D(1,0,10),…(2分) 则
设平面B1DC的法向量为
取y=1,得
∵
∴
∴
∴AC1∥平面B1DC;.…(4分) (Ⅱ)设平面BDC的法向量
则cosθ=|cos<
所以二面角B1-DC-B的余弦值为
(Ⅲ)假设线段A1C1上存在点E(0,y,2),(0<y<4),则
∵|cos<
∴cos60°=
整理得5y2-40y+36=0,∴y=4±
∵0<y<4,∴y=4-
∴
∴|
|
参考解析:
D
B1
【简答题】

[6/987]如图,若平面α⊥β,α∩β=CD,A∈α、B∈β,直线AB与α、β所成的角分别是30°、60°,则直线AB与CD所成角的大小为( ) A.60°B....
参考答案:
如图作BF⊥CD,AE⊥CD,AG∥EF,AG=EF,连接BE,FG,AF ∵平面α⊥β,∴AE⊥α,BF⊥β ∵直线AB与α、β所成的角分别是30°、60° ∴∠ABE=30°,∠BAF=60°, 设AB=2,则AE=1,AF=1, ∵△AEF为直角三角形, ∴E、F两点重合 ∴CD⊥平面ABE(F),AB⊂平面ABE(F), ∴CD⊥AB 即线AB与CD所成角的大小为90° 故选D |
参考解析:
无
【简答题】

[7/987]如图,在正方体ABCD-A1B1C1D1中,M、N分别是CD、CC1的中点,则异面直线A1M与DN所成的角的大小是( ...
参考答案:
| 90° |
参考解析:
无
【简答题】

[8/987]长方体 【图片】中, 【图片】则 【图片】所成的角的大小是 A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
A
|
参考解析:
连接
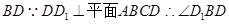 是
是
 所成的角,
所成的角,
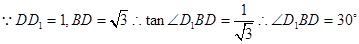
 所成的角的大小是
所成的角的大小是
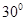
点评:斜线在平面上的射影与斜线所构成的夹角是斜线与平面所成的角,角的范围值
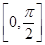
【简答题】

[9/987]如图,在长方体 【图片】中, 【图片】点 【图片】在棱 【图片】上. 【图片】 (1)求异面直线 【图片】与 【图片】所成的角; (2)若二面角 【图...
参考答案:
|
(1)对于异面直线的所成的角,一般采用平移法,平移到一个三角形中,借助于余弦定理求解。
(2) 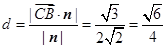
|
参考解析:
解法一:(1)连结
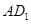 .由
.由
 是正方形知
是正方形知
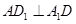 .
.
∵
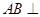 平面
平面
 ,
,
∴
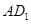 是
是
 在平面
在平面
 内的射影.
内的射影.
根据三垂线定理得
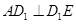 ,
,
则异面直线
 与
与
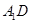 所成的角为
所成的角为
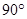 . 5分
. 5分
(2)作
 ,垂足为
,垂足为
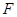 ,连结
,连结
 ,则
,则
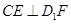 .
.
所以
 为二面角
为二面角
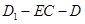 的平面角,
的平面角,
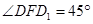 .于是
.于是
 ,
,
易得
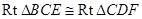 ,所以
,所以
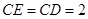 ,又
,又
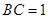 ,所以
,所以
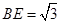 .
.
设点
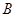 到平面
到平面
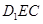 的距离为
的距离为
 ,则由于
,则由于
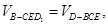 即
即
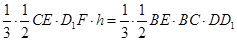 ,
,
因此有
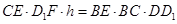 ,即
,即
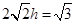 ,∴
,∴
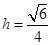 .…………12分
.…………12分
解法二:如图,分别以
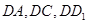 为
为
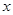 轴,
轴,
 轴,
轴,
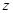 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
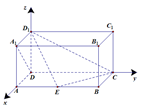
(1)由
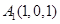 ,得
,得
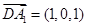 ,
,
设
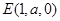 ,又
,又
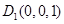 ,则
,则
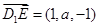 .
.
∵
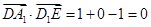 ∴
∴
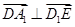 ,则异面直线
,则异面直线
 与
与
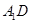 所成的角为
所成的角为
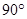 . 5分
. 5分
(2)
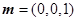 为面
为面
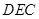 的法向量,设
的法向量,设
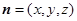 为面
为面
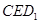 的法向量,则
的法向量,则
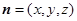
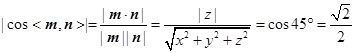 ,
,
∴
 . ①
. ①
由
 ,得
,得
 ,则
,则
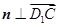 ,即
,即
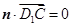 ,∴
,∴
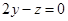
②由①、②,可取
 ,又
,又
 ,
,
所以点
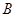 到平面
到平面
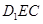 的距离
的距离
 . 12分
. 12分
点评:考查了异面直线所成的角以及点到面的距离的求解,属于基础题。
【简答题】

[10/987]如图,几何体 【图片】中,四边形 【图片】为菱形, 【图片】, 【图片】,面 【图片】∥面 【图片】, 【图片】、 【图片】、 【图片】都垂直于面 【...
参考答案:
|
(1)几何体
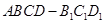 的体积为 的体积为
 ;(2)详见试题解析;(3)二面角 ;(2)详见试题解析;(3)二面角
 的大小为 的大小为
 . .
|
参考解析:
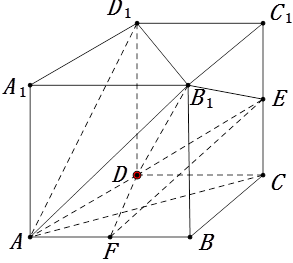
(1)将几何体
 补成如图的直四棱柱
补成如图的直四棱柱
 ,利用
,利用
 计算几何体
计算几何体
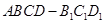 的体积;(2)详见试题解析;(3)取
的体积;(2)详见试题解析;(3)取
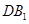 的中点
的中点
 ,因为
,因为
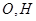 分别为
分别为
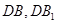 的中点,所以
的中点,所以
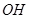 ∥
∥
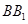 ,以
,以
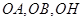 分别为
分别为
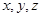 轴建立坐标系,利用法向量求二面角
轴建立坐标系,利用法向量求二面角
 的大小.
的大小.
(1)将几何体
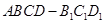 补成如图的直四棱柱
补成如图的直四棱柱
 ,则
,则
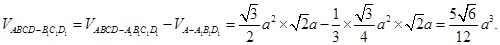 3分
3分
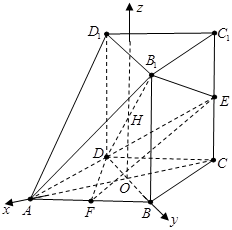
(2)连接
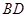 ,交
,交
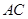 于
于
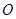 ,因为四边形
,因为四边形
 为菱形,
为菱形,
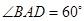 ,所以
,所以
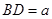 .因为
.因为
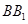 、
、
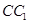 都垂直于面
都垂直于面
 ,
,

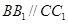 ,又面
,又面
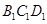 ∥面
∥面
 ,所以四边形
,所以四边形
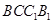 为平行四边形,则
为平行四边形,则
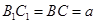 ,因为
,因为
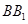 、
、
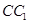 、
、
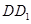 都垂直于面
都垂直于面
 ,则
,则
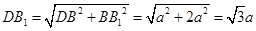 ,
,
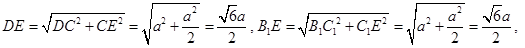 所以
所以
 ,所以
,所以
 为等腰直角三角形. 7分
为等腰直角三角形. 7分
(3)取
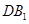 的中点
的中点
 ,因为
,因为
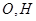 分别为
分别为
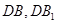 的中点,所以
的中点,所以
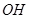 ∥
∥
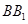 ,以
,以
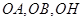 分别为
分别为
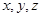 轴建立坐标系,则
轴建立坐标系,则
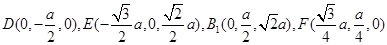 ,所以
,所以
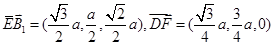 .
.
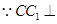 平面
平面
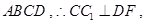
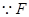 为的
为的
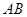 中点,
中点,
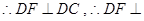 平面
平面
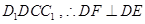 .由
.由
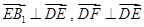 知二面角
知二面角
 的大小为
的大小为
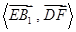 .
.
 二面角
二面角
 的大小为
的大小为
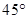 .
.
12分