下载APP

直线与平面垂直的判定与性质题库

题数
499
考试分类
高中数学>直线与平面垂直的判定与性质
售价
¥20
收藏
分享
去刷题



章节目录
简介
高中数学-直线与平面垂直的判定与性质
...更多
题目预览
【简答题】

[1/499]如图,四边形ABCD为矩形,AD⊥平面ABEAE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.(1)求证:AE⊥平面BCE;(...
参考答案:
| (1)证明:∵AD⊥平面ABE,AD∥BC, ∴BC⊥平面ABE, ∵AE⊂平面ABE, ∴AE⊥BC. 又∵BF⊥平面ACE,AE⊂平面ACE ∴BF⊥AE, ∵BC∩BF=B,∴AE⊥平面BCE (2)证明:连接GF,∵BF⊥平面ACE,∴BF⊥CE 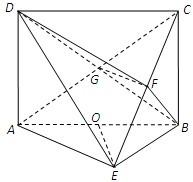 ∵BE=BC,∴F为EC的中点, ∵G是AC的中点, ∴FG∥AE ∵FG⊂平面BFD,AE⊄平面BFD ∴AE∥平面BFD; (3)取AB中点O,连接OE.因为AE=EB,所以OE⊥AB. 因为AD⊥面ABE,OE⊂面ABE,所以OE⊥AD,所以OE⊥面ADC 因为BF⊥面ACE,AE⊂面ACE,所以BF⊥AE. 因为CB⊥面ABE,AE⊂面ABE,所以AE⊥BC. 又BF∩BC=B,所以AE⊥平面BCE,又BE⊂面BCE,所以AE⊥EB. ∵AE=EB=2,∴AB=2 |
参考解析:
无
【简答题】

[2/499]ABCD是平面α内的一个四边形,P是平面α外的一点,则△PAB,△PBC,△PCD,△PDA中是直角三角形的最多有( ...
参考答案:
| 4 |
参考解析:
无
【简答题】

[3/499]已知:如图,在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点.求证:A1F⊥平面BED. 【图片】
参考答案:
| 证明:AA1⊥平面ABCD,AF是A1F在面ABCD上的射影 又∵AC⊥BD,∴A1F⊥BD 取BC中点G,连接FG,B1G, ∵A1B1⊥平面BCC1B1,FG⊥平面BCC1B1, ∴B1G为A1F在面BCC1B1上的射影, 又∵正方形BCC1B1中,E,G分别为CC1,BC的中点,∴BE⊥B1G, ∴A1F⊥BE又∵EB∩BD=B, ∴A1F⊥平面BED.  |
参考解析:
无
【简答题】

[4/499]如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形拆成一个四面体,使G1,G2,G...
参考答案:
| A |
参考解析:
无
【简答题】

[5/499]如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的 倍,P为侧棱SD上的点.(1)求证:AC⊥SD;(2)若SD⊥平面PAC...
参考答案:
| 证明:(1)连BD,设AC交于BD于O, 由题意知SO⊥平面ABCD. 以O为坐标原点,  分别为x轴、y轴、z轴正方向,建立坐标系O﹣xyz如图. 分别为x轴、y轴、z轴正方向,建立坐标系O﹣xyz如图.设底面边长为a,则高 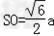 . .于是 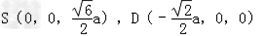 , , , ,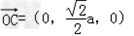 , ,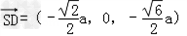 , ,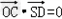 故OC⊥SD从而AC⊥SD (2)由题设知,平面PAC的一个法向量 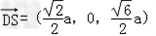 , ,平面DAC的一个法向量 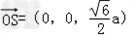 . .设所求二面角为θ,则 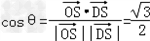 , ,所求二面角的大小为30°. (3)在棱SC上存在一点E使BE∥平面PAC. 由(2)知 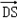 是平面PAC的一个法向量,且 是平面PAC的一个法向量,且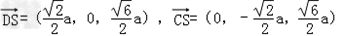 设 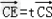 ,则 ,则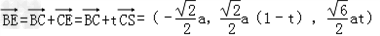 而 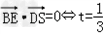 即当SE:EC=2:1时, 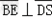 而BE不在平面PAC内, 而BE不在平面PAC内,故BE∥平面PAC  |
参考解析:
无
【简答题】

[6/499]如图,在四棱锥E﹣ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE.(1)求证:AE⊥BC;(2)如...
参考答案:
证明:(1)因为BM⊥平面ACE,AE 平面ACE, 平面ACE,所以BM⊥AE. 因为AE⊥BE,且BE∩BM=B,BE、BM  平面EBC, 平面EBC,所以AE⊥平面EBC. 因为BC  平面EBC, 平面EBC,所以AE⊥BC. (2)取DE中点H,连接MH、AH. 因为BM⊥平面ACE,EC  平面ACE, 平面ACE,所以BM⊥EC. 因为BE=BC,所以M为CE的中点. 所以MH为△EDC的中位线.所以MH∥  ,且MH= ,且MH= . .因为四边形ABCD为平行四边形, 所以DC∥AB,且DC=AB. 故MH∥  ,且MH= ,且MH=  . .因为N为AB中点, 所以MH∥AN,且MH=AN. 所以四边形ANMH为平行四边形, 所以MN∥AH. 因为MN  平面ADE,AH 平面ADE,AH 平面ADE, 平面ADE,所以MN∥平面ADE. |
参考解析:
无
【简答题】

[7/499]如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.求证:(1)PA∥平面BDE;(2)AC⊥平面PBD...
参考答案:
| 证明:(1)设AC∩BD=H,连接EH, 因为H为正方形ABCD对角线的交点,所以H为AC中点, 又E为PC中点, 所以EH为△PAC中位线, EH∥PA, EH⊂平面BDE,PA⊄平面BDE, 所以PA∥平面BDE. (2)因为AC、BD为正方形ABCD的对角线, 所以AC⊥BD, 又PD⊥平面ABCD,AC⊂平面ABCD, 所以PD⊥AC, 又PD∩BD=D, 所以AC⊥平面PDB. |
参考解析:
无
【简答题】

[8/499]m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是 [ ] A.若m∥α,n∥α,则m...
参考答案:
| D |
参考解析:
无
【简答题】

[9/499]如图所示的集合体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的.A,A′,B,B′分别为 【图片】CD, 【...
参考答案:
 证明:(1)∵A,A′分别为
连接BO2∵直线BO2是由直线AO1平移得到 ∴AO1∥BO2∴O1′A′∥BO2 ∴O1′,A′,O2,B共面. (2)将AO1延长至H使得O1H=O1A,连接HO1′,HB,H′H ∴由平移性质得O1′O2′=HB ∴BO2′∥HO1′, ∵A′G=H′O1′,H′H=A′H′,∠O1′H′H=∠GA′H′=
∴△GA′H′≌△O1′H′H, ∴∠H′O1′H+GH′A=
∴O1′H⊥H′G, ∴BO2′⊥H′G. ∵O1′O2′⊥B′O2′,O1′O2′⊥O2′O2,B′O2′∩O2′O2=O2′ ∴O1′O2′⊥平面B′BO2O2′ ∴O1′O2′⊥BO2′ ∴BO2′⊥H′B′, ∵H'B'∩H'G=H' ∴BO2′⊥平面H′B′G. |
参考解析:

CD
【简答题】

[10/499]如图,四棱柱ABCD-A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与...
参考答案:
| 解:(1)由已知AB=BC=2,∠ABC=60°, 则△ABC为正三角形, 所以AC=2 因为点O为AC的中点, 所以AO=1 又AA1=2,∠A1AO=60°, 在△A1OA中,由余弦定理,得   所以  所以A1O⊥AC 因为平面AA1C1C⊥平面ABCD,其交线为AC, 所以A1O⊥平面ABCD。 |
|
| (2)因为底面ABCD为菱形, ∴BD⊥AC 又BD⊥A1O, ∴BD⊥平面A1ACC1 如图,过点O作OE⊥AA1,垂足为E, 连接DE,则AA1⊥DE, 所以∠DEO为二面角D-AA1-C的平面角, 在Rt△AOD中,  在Rt△AEO中,  在Rt△DOE中,  故二面角D-AA1-C的平面角的正切值为2。 |
 |
参考解析:
无