
下载APP

直线的方程题库

题数
2000
考试分类
高中数学>直线的方程
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-直线的方程
...更多
题目预览
【简答题】

[1/2000]已知两条直线a1x+b1y+1=0和a2x+b2y+1=0都过点A(1,2),则过点P1(a1,b1),P2(a2,b2)的直线的方程是______.
参考答案:
| 把A(1,2)坐标代入两条直线a1x+b1y+1=0和a2x+b2y+1=0得 a1+2b1+1=0,a2+2b2+1=0, ∴a1-a2=2(b2-b1), 过点P1(a1,b1),P2(a2,b2)的直线的方程是:
-2(y-b1)=x-a1,x+2y-(a1+2b1)=0 ∵a1+2b1+1=0,a1+2b1=-1,∴所求直线方程为:x+2y+1=0 |
参考解析:
无
【简答题】

[2/2000]设a∈R,则“a=1”是“直线l 1:ax+2y-1=0与直线l 2:x+(a+1)y+4=0平行”的________条件.
参考答案:
|
充分不必要
|
参考解析:
无
【简答题】

[3/2000]已知两条直线l1:x+(3+m)y=2,l2:mx+2y=-8,若l1⊥l2,则m=______.
参考答案:
| 由直线垂直的条件可得,1×m+2(3+m)=0 ∴m=-2 故答案为:-2 |
参考解析:
无
【简答题】

[4/2000]已知A(4,0)B(1,-2)C(0,1)(1)求BC边上的高的方程.(2)求ABC的外接圆方程.
参考答案:
(1)kBC=
所以高所在直线的方程为:y-0=3(x-4)化简得y=3x-12; (2)先求圆心坐标:由(1)知直线BC的斜率为-
根据中点坐标公式得到(
联立求出公共解为圆心坐标(
再求圆的半径r:由两点间的距离公式得到r2=
则ABC的外接圆方程为:(x-
|
参考解析:
1-(-2)0-1
【简答题】

[5/2000]已知△ABC的顶点A(1,b),AB边上的中线CM所在直线方程为2x-b左+2=十,AC边上的高BH所在直线方程为2x+b左-9=十.求:(1)顶点C...
参考答案:
| 解(1)由多(1,图)及多C边上的高BH所在的直线方程2x+图y-9=2 得多C所在直线方程为图x-2y+图=2 又多B边上的中线CM所在直线方程为2x-图y+2=2 由
(2)设B(多,b),又多(1,图)M是多B的中点,则M(
由已知得
又C(-1,2)得直线BC的方程为x-qy+1=2 |
参考解析:
| 图x-2y+图=2 |
| 2x-图y+2=2 |
【简答题】

[6/2000]将直线 【图片】绕着它上面的一点 【图片】逆时针旋转 【图片】得直线 【图片】,则直线 【图片】的方程为 &nbs...
参考答案:
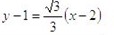
|
参考解析:
略
【简答题】

[7/2000]已知直线l1:3x+4y-2=0与l2:2x+y+2=0的交点为P.(Ⅰ)求交点P的坐标;(Ⅱ)求过点P且平行于直线l3:x-2y-1=0的直线方程;...
参考答案:
| (本小题满分12分) (Ⅰ)由
所以点P的坐标是(-2,2); …(4分) (Ⅱ)因为所求直线与l3平行, 所以设所求直线的方程为 x-2y+m=0. 把点P的坐标代入得-2-2×2+m=0,得m=6. 故所求直线的方程为x-2y+6=0; …(8分) (Ⅲ)因为所求直线与l3垂直, 所以设所求直线的方程为 2x+y+n=0. 把点P的坐标代入得 2×(-2)+2+n=0,得n=2. 故所求直线的方程为 2x+y+2=0. …(12分) |
参考解析:
| 3x+4y-2=0 |
| 2x+y+2=0 |
【简答题】

[8/2000]已知直线 【图片】平行,则k得值是( ) A. 1或3B.1或5C.3或5D.1或2
参考答案:
|
C
|
参考解析:
当k=3时,两直线平行,当k≠3时,由两直线平行,斜率相等,得:
 =k-3,解得:k=5,故选C。
=k-3,解得:k=5,故选C。
 =k-3,解得:k=5,故选C。
=k-3,解得:k=5,故选C。
【简答题】

[9/2000]己知点P在直线 【图片】上,点Q在直线 【图片】上, 【图片】中点 【图片】且 【图片】,则 【图片】的范围是( ...
参考答案:
|
C
|
参考解析:
无
【简答题】

[10/2000]A(1,3), B(5,-2),点 P在 x轴上使| AP|-| BP|最大,则 P的坐标为( ) A.(4,0)B...
参考答案:
|
B
|
参考解析:
因为B关于x轴的对称点M(5,2),所以
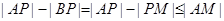 ,所以连接AM并延长交x轴对N点,则P与N重合时,
AP|-|
BP|最大,此时AM的直线方程为
,所以连接AM并延长交x轴对N点,则P与N重合时,
AP|-|
BP|最大,此时AM的直线方程为
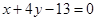 .令y=0,则x=13,所以点P的坐标为(13,0).
.令y=0,则x=13,所以点P的坐标为(13,0).
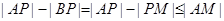 ,所以连接AM并延长交x轴对N点,则P与N重合时,
AP|-|
BP|最大,此时AM的直线方程为
,所以连接AM并延长交x轴对N点,则P与N重合时,
AP|-|
BP|最大,此时AM的直线方程为
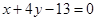 .令y=0,则x=13,所以点P的坐标为(13,0).
.令y=0,则x=13,所以点P的坐标为(13,0).