
下载APP

函数的极值与导数的关系题库

题数
2000
考试分类
高中数学>函数的极值与导数的关系
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-函数的极值与导数的关系
...更多
题目预览
【简答题】

[1/2000]函数f(x)=13x3+x2-3x-4的极小值是( ) A.-4B.-643C.-173D.-103
参考答案:
| 函数的导数为f'(x)=x2+2x-3=(x-1)(x+3), 由f'(x)>0,得x>1或x<-3,此时函数单调递增. 由f'(x)<0得-3<x<1,此时函数单调递减. 所以当x=-3时,函数取得极大值,当x=1时,函数取得极小值, 此时极小值为f(1)=
故选C. |
参考解析:
无
【简答题】

[2/2000]设a∈R,若函数y=eax+3x,x∈R有大于零的极值点,则 [ ] A.a>-3 B.a<-3C.a...
参考答案:
| B |
参考解析:
无
【简答题】

[3/2000]求曲线y= exx+1在点(1, e2)处的切线方程______.
参考答案:
由题意得,y′=
∴在点(1,
则所求的切线方程为:y-
故答案为:ex-4y+e=0. |
参考解析:
无
【简答题】

[4/2000]抛物线y= 14x2在点Q(2,1)处的切线方程是______.
参考答案:
∵y=
∴y'(x)=
所以曲线y=f(x)在点(2,1)处的切线方程为: y-1=1×(x-2),即x-y-1=0. 故答案为:x-y-1=0. |
参考解析:
无
【简答题】

[5/2000]已知 【图片】在 【图片】时取得极值,且 【图片】。(1)试求常数 【图片】值;(2)试判断 【图片】是函数的极小值还是极大值,并说明理由。
参考答案:
|
⑴
 ⑵当 ⑵当
 时, 时,
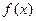 取得极大值,当 取得极大值,当
 , ,
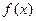 取得极小值。 取得极小值。
|
参考解析:
(1)
 ,∴
,∴
 即
即
 ,解得
,解得
 ,∴
,∴
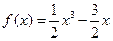 。
。
(2)
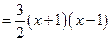 ,令
,令
 得
得
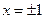 ,列表如下:
,列表如下:
由表知,当
 时,
时,
 取得极大值,当
取得极大值,当
 ,
,
 取得极小值。
取得极小值。
 ,∴
,∴
 即
即
 ,解得
,解得
 ,∴
,∴
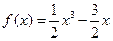 。
。
(2)

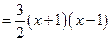 ,令
,令
 得
得
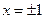 ,列表如下:
,列表如下:
 |
 |
 |
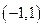 |
 |
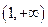 |
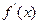 |
+ |
0 |
- |
0 |
+ |
 |
增 |
极大值 |
减 |
极小值 |
增 |
 时,
时,
 取得极大值,当
取得极大值,当
 ,
,
 取得极小值。
取得极小值。
【简答题】

[6/2000]设a∈R,若函数y=ex+ax,x∈R,有大于零的极值点,则( ) A.a<-1 B.a>-1 C.a<- 1 e D.a>- 1 e
参考答案:
| 解:∵y=ex+ax, ∴y'=ex+a.由题意知ex+a=0有大于0的实根, 令y1=ex,y2=-a,则两曲线交点在第一象限,结合图象易得-a>1?a<-1, 故选A.  |
参考解析:
无
【简答题】

[7/2000]已知函数 【图片】取得极小值 【图片】. (Ⅰ)求a,b的值; (Ⅱ)设直线 【图片】. 若直线 l与曲线 S同时满足下列两个条件: (1)直线 l与...
参考答案:
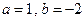 , ,
|
参考解析:
解:(I)因为
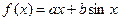 ,所以
,所以

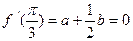 ,
,
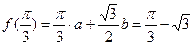
解得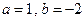 ,
,
此时 ,当
,当
 时
时
 ,当
,当
 时
时
 ,
,
所以 时
时
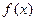 取极小值,所以
取极小值,所以
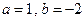 符合题目条件;
符合题目条件;
(II)由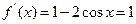 得
得
 ,
,
当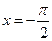 时,
时,
 ,此时
,此时
 ,
,
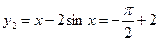 ,
,
 ,所以
,所以
 是直线
是直线
 与曲线
与曲线
 的一个切点;
的一个切点;
当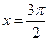 时,
时,
 ,此时
,此时
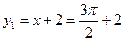 ,
,
 ,
,
 ,所以
,所以
 是直线
是直线
 与曲线
与曲线
 的一个切点;
的一个切点;
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,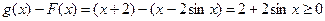 ,所以
,所以
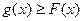
因此直线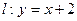 是曲线
是曲线
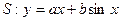 的“上夹线”.
的“上夹线”.
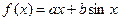 ,所以
,所以

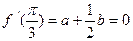 ,
,
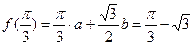
解得
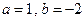 ,
,
此时
 ,当
,当
 时
时
 ,当
,当
 时
时
 ,
,
所以
 时
时
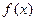 取极小值,所以
取极小值,所以
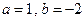 符合题目条件;
符合题目条件;
(II)由
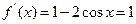 得
得
 ,
,
当
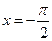 时,
时,
 ,此时
,此时
 ,
,
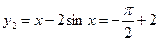 ,
,
 ,所以
,所以
 是直线
是直线
 与曲线
与曲线
 的一个切点;
的一个切点;
当
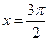 时,
时,
 ,此时
,此时
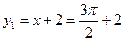 ,
,
 ,
,
 ,所以
,所以
 是直线
是直线
 与曲线
与曲线
 的一个切点;
的一个切点;
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,
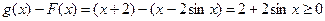 ,所以
,所以
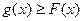
因此直线
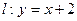 是曲线
是曲线
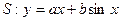 的“上夹线”.
的“上夹线”.
【简答题】

[8/2000]已知极限limn→∞(n•sin1n)=1,则极限limn→∞2n-n2sin 1n2n-1=______.
参考答案:
故答案为:
|
参考解析:
limn→∞
【简答题】

[9/2000]计算limn→∞2n2+11+2+…+n=______.
参考答案:
∵1+2+3+…+n=
∴
∴
故答案为4. |
参考解析:
n(n+1)2
【简答题】

[10/2000](本小题满分12分) 已知函数 【图片】的图象在 【图片】处的切线与 【图片】轴平行. (1)求 【图片】与 【图片】的关系式及 f( x)的极大值;...
参考答案:
|
(1)
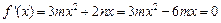 ,极大值为
f(0)=0 ,极大值为
f(0)=0
(2) 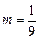
|
参考解析:
解:(1)由图象在
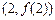 处的切线与
x轴平行,知
处的切线与
x轴平行,知
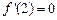
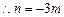 ,
,
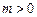 ①………………………………………
①………………………………………
 ……… (3分)
……… (3分)
令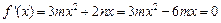
得 易证
易证
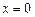 是
是
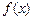 的极大值点,
的极大值点,
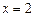 是极小值点.
是极小值点.
极大值为 f(0)="0;" …………………………………………………(6分)
(2) 令 .
.
(I)当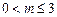 时,
时,
 ②
②
由①
 ,②解得
,②解得
 ,符合前提
,符合前提
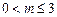 .
.
(II)当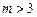 时,
时,

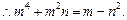 ③
③
由①,③得 m 3-3 m 2+9 m-1=0,
∵ m>3时, m 3-3 m 2+9 m-1= m 2( m-3)+9 m-1>0
∴ m 3-3 m 2+9 m-1=0在 上无实数根.
上无实数根.
 综上讨论可知,
m的值为
综上讨论可知,
m的值为
 .……………………………………(12分)
.……………………………………(12分)
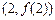 处的切线与
x轴平行,知
处的切线与
x轴平行,知
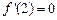
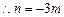 ,
,
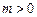 ①………………………………………
①………………………………………
 ……… (3分)
……… (3分)
令
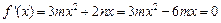
得
 易证
易证
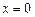 是
是
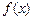 的极大值点,
的极大值点,
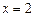 是极小值点.
是极小值点.
极大值为 f(0)="0;" …………………………………………………(6分)
(2) 令
 .
.
(I)当
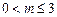 时,
时,
 ②
②
由①

 ,②解得
,②解得
 ,符合前提
,符合前提
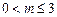 .
.
(II)当
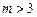 时,
时,

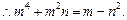 ③
③
由①,③得 m 3-3 m 2+9 m-1=0,
∵ m>3时, m 3-3 m 2+9 m-1= m 2( m-3)+9 m-1>0
∴ m 3-3 m 2+9 m-1=0在
 上无实数根.
上无实数根.
 综上讨论可知,
m的值为
综上讨论可知,
m的值为
 .……………………………………(12分)
.……………………………………(12分)