
下载APP

一次函数的性质与应用题库

题数
1187
考试分类
高中数学>一次函数的性质与应用
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-一次函数的性质与应用
...更多
题目预览
【简答题】

[1/1187](本题满分14分)已知函数 【图片】的图像过点(1,3),且 【图片】对任意实数都成立,函数 【图片】与 【图片】的图像关于原点对称. (Ⅰ)求 【图...
参考答案:
|
(1) 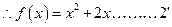 , ,
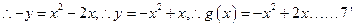
(2) 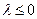
|
参考解析:
解:⑴由题意知:
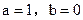 ,
,
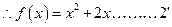
设函数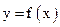 图象上的任意一点
图象上的任意一点
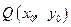 关于原点的对称点为P(x,y),
关于原点的对称点为P(x,y),
则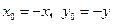 , ……………………4分
, ……………………4分
因为点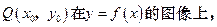
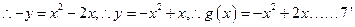
⑵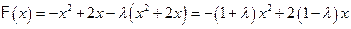
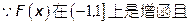 连续,
连续,
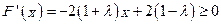 恒成立……9分
恒成立……9分
即 ,………………..10分
,………………..10分
由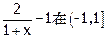 上为减函数,………………..12分
上为减函数,………………..12分
当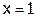 时取最小值0,………………..13分
时取最小值0,………………..13分
故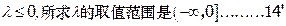
另解: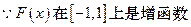 ,
,
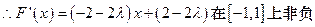
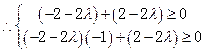 ,解得
,解得
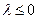
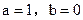 ,
,
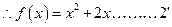
设函数
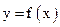 图象上的任意一点
图象上的任意一点
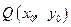 关于原点的对称点为P(x,y),
关于原点的对称点为P(x,y),
则
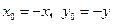 , ……………………4分
, ……………………4分
因为点
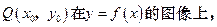
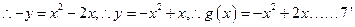
⑵
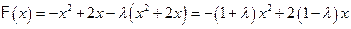
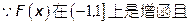 连续,
连续,
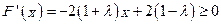 恒成立……9分
恒成立……9分
即
 ,………………..10分
,………………..10分
由
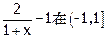 上为减函数,………………..12分
上为减函数,………………..12分
当
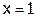 时取最小值0,………………..13分
时取最小值0,………………..13分
故
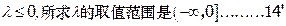
另解:
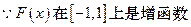 ,
,
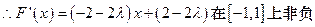
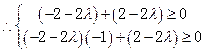 ,解得
,解得
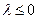
【简答题】

[2/1187]已知一次函数f(x)是减函数,且满足f[f(x)]=4x-1,则f(x)=( )
参考答案:
| -2x+1 |
参考解析:
无
【简答题】

[3/1187]已知函数 【图片】当 【图片】,求 【图片】的解析式;
参考答案:
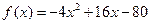
|
参考解析:
据题意:
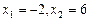 是方程
是方程
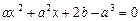 的两根
的两根
由韦达定理知: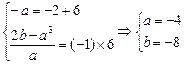
故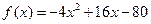
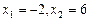 是方程
是方程
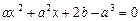 的两根
的两根
由韦达定理知:
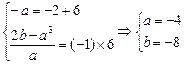
故
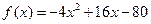
【简答题】

[4/1187]若 【图片】, 【图片】恒成立,则 【图片】得范围是 .
参考答案:
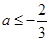
|
参考解析:
原不等式可化成
 ,令
,令

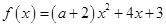
则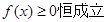 ,则
,则
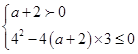 ,解得
,解得
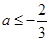
 ,令
,令

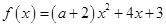
则
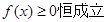 ,则
,则
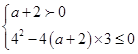 ,解得
,解得
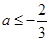
【简答题】

[5/1187]已知函数 【图片】,或 【图片】,且 【图片】,则 A. 【图片】B. 【图片】C. 【图片】D. 【图片】与 【图片】的大小不能确定
参考答案:
|
C
|
参考解析:
因为二次函数的性质,对称轴为x=2,那么可知两个变量和与对称轴的关系,可知x
1离开对称轴的距离要比x
2离开对称轴的距离要远,选C
【简答题】

[6/1187]求函数 【图片】的值域。
参考答案:
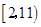
|
参考解析:
思路分析:
1)题意分析:求二次函数在指定区间上的值域
2)解题思路:配方,画图,找区间
解:配方,得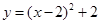 ,又
,又
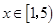 ,结合图象,知函数的值域是
,结合图象,知函数的值域是
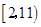 。
。
解题后的思考:“配方,画图,找区间”适用于解析式为二次函数的题目。
1)题意分析:求二次函数在指定区间上的值域
2)解题思路:配方,画图,找区间
解:配方,得
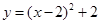 ,又
,又
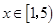 ,结合图象,知函数的值域是
,结合图象,知函数的值域是
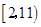 。
。
解题后的思考:“配方,画图,找区间”适用于解析式为二次函数的题目。
【简答题】

[7/1187](本题满分12分) 已知函数 【图片】( 【图片】), (1)求函数 【图片】的最小值; (2)已知 【图片】,命题 p:关于 x的不等式 【图片】对...
参考答案:
|
解:(1)由
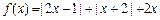 得 得
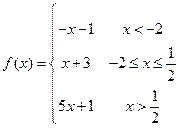 ,作函数 ,作函数
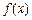 的图象 的图象
由图可知 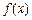 在 在
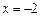 处有最小值 处有最小值
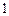 ………5分 ………5分
(2)由(1)知: 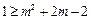 ,解得 ,解得
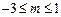
所以命题 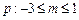 ………7分 ………7分
对于命题 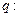 不等式 不等式
 对任意 对任意
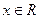 恒成立, 恒成立,
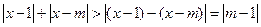
∴ 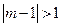 ,即 ,即
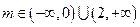 , ………9分 , ………9分
而“ p或 q”为真,“ p且 q”为假,可知命题 p与命题 q一真一假。 若“ p真 q假”时,则 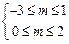 ,解得 ,解得
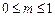
若“ p假 q真”时,则 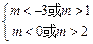 ,解得 ,解得
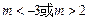
故实数 m的取值范围是 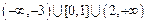 ………12分 ………12分
|
参考解析:
略
【简答题】

[8/1187]定义运算: 【图片】,例如: 【图片】, 【图片】,则函数 【图片】的最大值为____________.
参考答案:
|
4
|
参考解析:
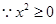 且当
且当
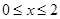 时,
时,
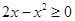 ;当
;当
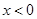 或
或
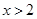 时,
时,
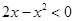
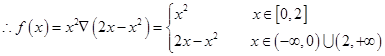
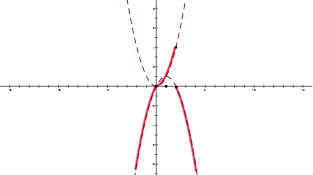
易知:当
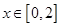 时,
时,
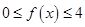
当
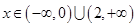 时,
时,
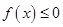
所以
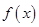 的最大值是4.
的最大值是4.
【简答题】

[9/1187]函数 【图片】与函数 【图片】的图象可能是( ) 【图片】A B C &nbs...
参考答案:
|
C
|
参考解析:
D中
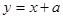 的截距
的截距
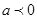 ,而
,而
 中
中
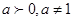 排除D;
排除D;
A中
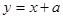 的截距
的截距
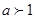 ,
,
 是减函数,
是减函数,
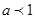 ,;
,;
B中
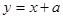 的截距
的截距
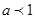 ,
,
 是增函数,
是增函数,
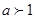 ;
;
C中
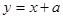 的截距
的截距
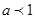 ,
,
 是减函数,
是减函数,
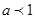 ;
;
【简答题】

[10/1187]..(满分12分) 已知二次函数 【图片】的图像经过坐标原点,其导函数为 【图片】,数列 【图片】的前 【图片】项和为 【图片】,点 【图片】 【图片...
参考答案:
|
解:1)由题可设 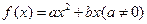 ,则 ,则
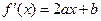 ,由 ,由
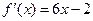 得 得
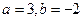 ,所以 ,所以
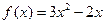 …………2分 …………2分
又由点 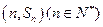 均在函数 均在函数
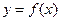 的图像上,得 的图像上,得
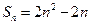 …………3分 …………3分
当 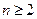 时, 时,
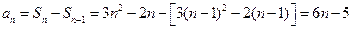 …………5分 …………5分
当 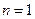 时, 时,
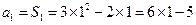
所以 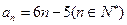 ………………6分 ………………6分
2)由1)得 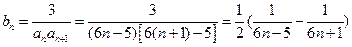 …………8分 …………8分
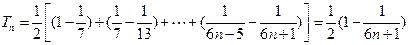 …………10分 …………10分
因此使得 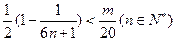 成立的 成立的
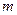 仅需且必须满足 仅需且必须满足
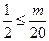 ,即 ,即
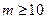
故满足要求的最小正整数 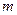 为10。………………12分 为10。………………12分
|
参考解析:
略