
下载APP

函数的奇偶性、周期性题库

题数
2000
考试分类
高中数学>函数的奇偶性、周期性
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-函数的奇偶性、周期性
...更多
题目预览
【简答题】

[1/2000]若f(x)是以5为周期的奇函数且f(-3)=1,tanα=2,则f(20sinαcosα)=______.
参考答案:
∵20sinα•cosα=10sin2α=10×
∴f(20sinαcosα)=f(8)=f(3)=-f(-3)=-1 故答案为:-1 |
参考解析:
2tanα1+
tan2α
【简答题】

[2/2000]若函数f(x)= x2-9x-3(x≠3)a(x=3)在x=3处连续,则a=______.
参考答案:
由函数连续的定义可得,
∴
∴
故答案为:6 |
参考解析:
无
【简答题】

[3/2000]函数 【图片】 [ ] A.是奇函数 不是偶函数 B.是偶函数,不是奇函数 C.既是奇函数,又是偶函数...
参考答案:
| A |
参考解析:
无
【简答题】

[4/2000]已知函数f(x)=ax-a+1,(a>0且a≠1)恒过定点(3,2),(1)求实数a;(2)在(1)的条件下,将函数f(x)的图象向下平移1个单位,再...
参考答案:
| (1)由f(x)=ax-a+1,知令x=a,则f(a)=2, 所以f(x)恒过定点(a,2), 由题设得a=3; (2)由(1)知f(x)=3x-3+1, 将f(x)的图象向下平移1个单位,得到m(x)=3x-3, 再向左平移3个单位,得到g(x)=3x, 所以函数g(x)的反函数h(x)=log3x. (3)[h(x)+2]2≤h(x2)+m+2,即[log3x+2]2≤log3x2+m+2, 所以(log3x)2+2log3x+2-m≤0, 令t=log3x,则由x∈[1,9]得t∈[0,2], 则不等式化为t2+2t+2-m≤0, 不等式[h(x)+2]2≤h(x2)+m+2 恒成立,等价于t2+2t+2-m≤0恒成立, 因为t2+2t+2-m=(t+1)2+1-m在[0,2]上单调递增, 所以t2+2t+2-m≤22+2×2+2-m=10-m, 所以10-m≤0,解得m≥10. 故实数m的取值范围为:m≥10. |
参考解析:
无
【简答题】

[5/2000]已知函数f(x)= ax+b1+x2是定义在(-1,1)上的奇函数,且f( 12)= 25,①求函数f(x)的解析式;②判断函数f(x)在(-1,1)...
参考答案:
①依题意得
∴f(x)=
②f(x)在(-1,1)上是增函数, 证明如下:任取-1<x1<x2<1, 则f(x1)-f(x2)=
∵-1<x1<x2<1 ∴x1-x2<0,1-x1x2>0 ∴f(x1)-f(x2)<0,即f(x1)<f(x2). ∴f(x)在(-1,1)上是增函数. ③令log2x=t,则不等式f(log2x-1)+f(log2x)<0, 转化为f(t-1)+f(t)<0⇒f(t-1)<-f(t)=f(-t). ∵f(x)在(-1,1)上是增函数; ∴-1<t-1<-t<1⇒0<t<
∴0<log2x<
∴不等式f(log2x-1)+f(log2x)的解集为(1,
|
参考解析:
无
【简答题】

[6/2000]若 【图片】是奇函数,则 【图片】= ;
参考答案:
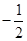 . .
|
参考解析:
因为
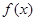 为奇函数,所以
为奇函数,所以
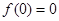 ,所以
,所以
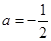
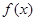 为奇函数,所以
为奇函数,所以
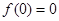 ,所以
,所以
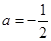
【简答题】

[7/2000]设f0(x)=sin x,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2010(x)=...
参考答案:
| ∵f1(x)=(sinx)′=cosx, f2(x)=(cosx)′=-sinx, f3(x)=(-sinx)′=-cosx, f4(x)=(-cosx)′=sinx, f5(x)=(sinx)′=f1(x),f6(x)=f2(x),. ∴fn+4(x)=fn(x),即周期T为4. ∴f2010(x)=f2(x)=-sinx. 故答案为:-sinx |
参考解析:
无
【简答题】

[8/2000]已知函数f(x)是(-∞,+∞)上的偶函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-20...
参考答案:
| C |
参考解析:
无
【简答题】

[9/2000]若f(x)=1- a2x-1是奇函数,则a的值为______.
参考答案:
f(-x)=1-
∵f(x)为奇函数 ∴f(-x)=-f(x) ∴1-
解得a=-2 故答案为-2 |
参考解析:
无
【简答题】

[10/2000]已知函数f(x)= 【图片】,若f(a)= 【图片】,则f(-a)=________.
参考答案:
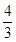
|
参考解析:
根据题意,f(x)=
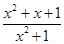 =1+
=1+
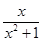 ,而h(x)=
,而h(x)=
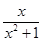 是奇函数,
是奇函数,
故f(-a)=1+h(-a)=1-h(a)=2-
[1+h(a)]=2-f(a)=2-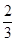 =
=
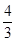 .
.
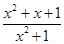 =1+
=1+
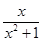 ,而h(x)=
,而h(x)=
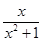 是奇函数,
是奇函数,
故f(-a)=1+h(-a)=1-h(a)=2-
[1+h(a)]=2-f(a)=2-
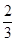 =
=
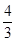 .
.