logo - 刷刷题
下载APP
直线与椭圆方程的应用题库
直线与椭圆方程的应用题库 - 刷刷题
题数
331
考试分类
高中数学>直线与椭圆方程的应用
售价
¥20
收藏
分享
去刷题
章节目录
简介
高中数学-直线与椭圆方程的应用
...更多
题目预览
【简答题】
[1/331]设椭圆的中心是坐标原点，长轴在x轴上，离心率e=32，已知点P（0， 32）到这个椭圆上的点最远距离是7．求这个椭圆的方程，并求椭圆上到点P的距离等于...
参考答案：

魔方格
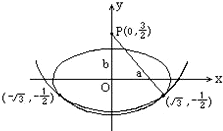根据题设条件，可取椭圆的参数方程是
x=acosθ
y=bsinθ
，其中0≤θ＜2π，
由e2=
c2
a2
=1-(
b
a
)2可得
b
a
=
1-e2
=
1-
3
4
=
1
2
，即a=2b．
设椭圆上的点（x，y）到点P的距离为d，则
d2=x2+(y-
3
2
)2
=a2cos2θ+(bsinθ-
3
2
)2
=a2-(a2-b2) sin2θ-3bsinθ+
9
4

=4b2-3b2sin2θ-3bsinθ+
9
4

=-3b2(sinθ+
1
2b
)2+4b2+3．
如果
1
2b
＞1 ，即b＜
1
2
，则当sinθ=-1时，d2有最大值，由题设得(
7
)2=(b+
3
2
)2，
由此得b=
7
-
3
2
＞
1
2
，与b＜
1
2
矛盾．
因此必有
1
2b
≤1 成立，于是当sinθ=-
1
2b
时，d2有最大值，由题设得(
7
)2=4b2+3，
由此可得b=1，a=2．
所求椭圆的参数方程是
x=2cosθ
y=sinθ
，由sinθ=-
1
2
，cosθ=±
3
2
可得，
椭圆上的点(-
3
，-
1
2
)和(
3
，-
1
2
)到点P的距离都是
7
．
参考解析：
无
【简答题】
[2/331]椭圆C： 【图片】的两个焦点为F1，F2，点P在椭圆C上，且PF1⊥F1F2，|PF1|= 【图片】，|PF2|= 【图片】。（1）求椭圆C的方程；（...
参考答案：

解：（1）因为点P在椭圆C上，所以2a=|PF1|+|PF2|=6，a=3．
在Rt△PF1F2中，，
故椭圆的半焦距c=，从而
b2=a2﹣c2=4，所以椭圆C的方程为=1．
（2）设A，B的坐标分别为（x1，y1）、（x2，y2）．
已知圆的方程为（x+2）2+（y﹣1）2=5，
所以圆心M的坐标为（﹣2，1）．
从而可设直线l的方程为y=k（x+2）+1，
代入椭圆C的方程得（4+9k2）x2+（36k2+18k）x+36k2+36k﹣27=0．
因为A，B关于点M对称．
所以
解得，
所以直线l的方程为，
即8x﹣9y+25=0．（经检验，所求直线方程符合题意）
参考解析：
无
【简答题】
[3/331]已知椭圆E： 【图片】，对于任意实数k，下列直线被椭圆E截得的弦长与l：y=kx+1被椭圆E截得的弦长不可能相等的是（   ） A．kx+y...
参考答案：
D
参考解析：
无
【简答题】
[4/331]设F是椭圆x27+ y26=1的右焦点，且椭圆上至少有21个不同的点Pi（i=1，2，3，…），使|FP1|，|FP2|，|FP3|，…组成公差为d的...
参考答案：
若这个等差数列是增数列，则a1≥|FP1| =
7
-1，a21≤|FP21| =
7
+1，
∴a21=a1+20d，∴0＜a21-a1=20d≤(
7
+1)-(
7
-1)=2，
解得0＜d≤
1
10
．
若这个等差数列是减数列，则a1≤ |FP1|=
7
+1，a21≥ |FP2|=
7
-1，
∴a21=a1+20d，∴0＞a21-a1=20d≥(
7
-1) -(
7
+1)=-2，
解得-
1
10
≤d＜0．
∴d的取值范围为[-
1
10
，0)∪(0，
1
10
]．
答案：[-
1
10
，0)∪(0，
1
10
]．
参考解析：
7
【简答题】
[5/331]在平面直角坐标系xoy中，已知△ABC顶点A（-1，0）和C（1，0），顶点B在椭圆上 【图片】，则 【图片】的值是（　　） A．0 B．1 C．2 ...
参考答案：
C
参考解析：
无
【简答题】
[6/331]经过点M（-2，1）作直线l交椭圆x26+ y24=1于S、T两点，且M是ST的中点，求直线l的方程．
参考答案：
设S（x1，y1）T（x2，y2），
∵点M（-2，1）是ST的中点，
∴x1+x2=-4，y1+y2=2，
把S（x1，y1）T（x2，y2）代入2x2+3y2=12，得
2x12+3y12=12
2x22+3y22=12
，
∴2（x1+x2）（x1-x2）+3（y1+y2）（y1-y2）=0，
∴-8（x1-x2）+6（y1-y2）=0，
∴k=
y1-y2
x1-x2
=
4
3
，
∴直线l的方程：y-1=
4
3
(x+2)，
整理，得4x-3y+11=0．
参考解析：
无
【简答题】
[7/331]某海域内有一孤岛，岛四周的海平面（视为平面）上有一浅水区（含边界），其边界是长轴长为2a，短轴长为2b的椭圆，已知岛上甲、乙导航灯的海拔高度分别为h1...
参考答案：
依题意，|MF1|+|MF2|≤2a?h1?cotθ1+h2?cotθ2≤2a；
故答案为：h1?cotθ1+h2?cotθ2≤2a
参考解析：
无
【简答题】
[8/331]”m＞n＞0”是”方程mx2+ny2=1表示焦点在y轴上的椭圆”的（   ） A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．...
参考答案：
C
参考解析：
无
【简答题】
[9/331]已知点A（-2，0）在椭圆 【图片】上，设椭圆E与y轴正半轴的交点为B，其左焦点为F，且∠AFB=150°．（1）求椭圆E的方程；（2）过x轴上一点M...
参考答案：
解：（1）∵∠AFB=150°
∴∠OFB=30°（O为坐标原点）在直角△BOF中，|FB|=2|OB|
∵a=2b ∵点A（﹣2，0）在椭圆上
∴a=2  ∴b=1  ∴椭圆；
（2）∵直线l过x轴上一点M（m，0）（m≠﹣2）不垂直于y轴
∴l：x=ty+m与椭圆方程联立
消元整理可得（t2+4）y2+2mty+m2﹣4=0
∴△=4m2t2﹣4（t2+4）（m2﹣4）＞0
∴t2＞m2﹣4设C（x1，y1），D（x2，y2）
∴，
（i）若以CD为直径的圆恒过A点，则∵=（x1+2，y1），=（x2+2，y2）
∴x1x2+2（x1+x2）+4+y1y2=
∴或m=﹣2（舍去）
∴实数m的值为；
（ii）若△ACD的重心恒在y轴的左侧，即重心的横坐标恒小于0，即，∴
∴4m＜t2+4对所有符合条件的t恒成立
由t2＞m2﹣4知：
①若m2﹣4＜0，即﹣2＜m＜2时，t2∈[0，+∞）
∴t2+4≥4   ∴m＜1   ∴﹣2＜m＜1；
②若m2﹣4≥0，即m≤﹣2或m≥2时，t2∈（m2﹣4，+∞），∴4m＜m2，∴m≤0或m≥4
综上知，实数m的取值范围是（﹣∞，﹣2）∪（﹣2，1）∪[4，+∞）
参考解析：
无
【简答题】
[10/331]椭圆 【图片】上的点到直线 【图片】的最大距离是 [     ] A．3   B． 【图片...
参考答案：
D
参考解析：
无