
下载APP

导数的运算题库

题数
2000
考试分类
高中数学>导数的运算
售价
¥30
收藏
分享
去刷题



章节目录
简介
高中数学-导数的运算
...更多
题目预览
【简答题】

[1/2000]已知函数 【图片】. (Ⅰ)若 【图片】,且对于任意 【图片】恒成立,试确定实数 【图片】的取值范围; (Ⅱ)设函数 【图片】, 求证: 【图片】
参考答案:
|
(Ⅰ)
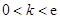 (Ⅱ)详见解析 (Ⅱ)详见解析
|
参考解析:
(Ⅰ)
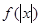 是偶函数,只需研究
是偶函数,只需研究
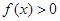 对任意
对任意
 成立即可,即当
成立即可,即当
 时
时
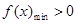
(Ⅱ)观察结论,要证
 ,即证
,即证
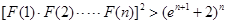 ,变形可得
,变形可得
 ,
,
可证

 .问题得以解决.
.问题得以解决.
(Ⅰ)由
 可知
可知
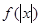 是偶函数.
是偶函数.
于是
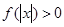 对任意
对任意
 成立等价于
成立等价于
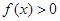 对任意
对任意
 成立. (1分)
成立. (1分)
由
 得
得
 .
.
①当
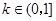 时,
时,
 .
.
此时
 在
在
 上单调递增. 故
上单调递增. 故
 ,符合题意.(3分)
,符合题意.(3分)
②当
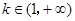 时,
时,
 .
.
当
 变化时
变化时
 的变化情况如下表: (4分)
的变化情况如下表: (4分)
 |
 |
 |
 |
 |
 |
 |
 |
 |
单调递减 |
极小值 |
单调递增 |
 上,
上,
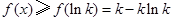 .
.
依题意,
 ,又
,又
 .
.
综合①,②得,实数
 的取值范围是
的取值范围是
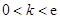 . (7分)
. (7分)
(Ⅱ)
 ,
,

又

 ,
,
(10分)
 ,
,
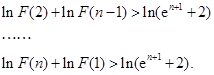 (12分)
(12分)
由此得:
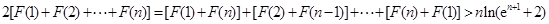
故
 成立. (14分).
成立. (14分).
【简答题】

[2/2000]已知 【图片】是实数,函数 【图片】, 【图片】和 【图片】,分别是 【图片】的导函数,若 【图片】在区间 【图片】上恒成立,则称 【图片】和 【图片...
参考答案:
|
(Ⅰ)
 ;(Ⅱ) ;(Ⅱ)
 . .
|
参考解析:
(Ⅰ)由不等式恒成立,即可求出结果. (Ⅱ)
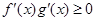 在以
在以
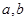 为端点的开区间上恒成立,对
为端点的开区间上恒成立,对
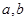 的大小分类讨论,以确定
的大小分类讨论,以确定
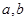 的取值范围,从而去确定
的取值范围,从而去确定
 的最大值.
的最大值.
由已知,
 ,
,
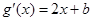 ,
,
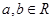 ;
;
(Ⅰ)由题设“单调性一致”定义知,
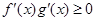 在区间
在区间
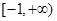 上恒成立,
上恒成立,
即
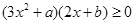 在区间
在区间
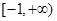 上恒成立,
上恒成立,
因
 ,所以
,所以
 ,所以,
,所以,
 在区间
在区间
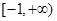 上恒成立,
上恒成立,
即
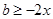 在区间
在区间
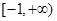 上恒成立,而
上恒成立,而
 在
在
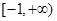 上最大值
上最大值

所以,
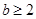 ,即
,即
 ;
;
(Ⅱ)由“单调性一致”定义知,
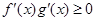 在以
在以
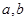 为端点的开区间上恒成立,
为端点的开区间上恒成立,
即
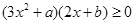 在以
在以
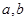 为端点的开区间上恒成立,
为端点的开区间上恒成立,
因
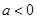 ,所以,由
,所以,由
 ,得
,得
 ,
,
 ,
,
 ;
;
①若
 ,则开区间为
,则开区间为
 ,取
,取
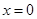 ,由
,由
 知,
知,
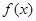 和
和
 在区间
在区间
 上单调性不一致,不符合题设;
上单调性不一致,不符合题设;
②若
 ,因
,因
 均为非负,故不在以
均为非负,故不在以
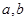 为端点的开区间内;所以,只有可能
为端点的开区间内;所以,只有可能
 在区间上;
在区间上;
由
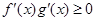 在以
在以
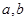 为端点的区间上恒成立,知
为端点的区间上恒成立,知
 要么不小于
要么不小于
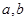 中的大者,要么不大于
中的大者,要么不大于
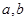 中的小者;
中的小者;
因为
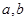 都不大于0,所以,
都不大于0,所以,
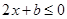 ,所以,由
,所以,由
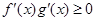 知
知
 ,所以
,所以
 ;
;
当
 时,由
时,由
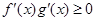 在区间
在区间
 上恒成立,即
上恒成立,即
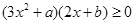 在区间
在区间
 上恒成立,知
上恒成立,知
 最大值为
最大值为
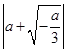 ,而由
,而由
 解得
解得
 ;
;
此时,
 ,配方后知,取不到最大值;
,配方后知,取不到最大值;
当
 时,显然,此时,当
时,显然,此时,当
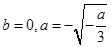 ,即
,即
 时,
时,
 取得最大值
取得最大值
 ;综上,
;综上,
 的最大值为
的最大值为
 .
.
【简答题】

[3/2000]已知 【图片】,则 【图片】 &...
参考答案:

|
参考解析:
解:因为
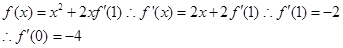
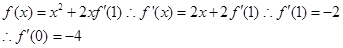
【简答题】

[4/2000]已知函数 【图片】. (1)当 【图片】时,求函数 【图片】的单调区间; (2)当 【图片】时,若 【图片】, 【图片】恒成立,求实数 【图片】的最小...
参考答案:
|
(1)
 的单减区间是 的单减区间是
 ,单增区间是 ,单增区间是
 ;(2) ;(2)
 ;(3)详见解析. ;(3)详见解析.
|
参考解析:
(1)函数问题先求定义域
 ,当
,当
 时,由于函数
时,由于函数
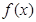 中含有绝对值符号,故要考虑
中含有绝对值符号,故要考虑
 或
或
 两种情况,接着求分别
两种情况,接着求分别
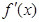 ,令
,令
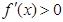 ,
,
 求出其单调增区间或减区间;(2)当
求出其单调增区间或减区间;(2)当
 时,
时,
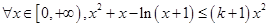 ,即
,即
 ,构造新函数
,构造新函数
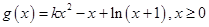 ,用导数法求函数
,用导数法求函数
 的最小值,必须对
的最小值,必须对
 分类讨论,从而求出
分类讨论,从而求出
 的最小值;(3)由(2)得,
的最小值;(3)由(2)得,
 ,当
,当
 时,不等式左边
时,不等式左边
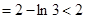 ,所以不等式成立,当
,所以不等式成立,当
 时,令
时,令
 代入
代入
 ,用放缩法证明不等式成立.
,用放缩法证明不等式成立.
(1)当
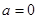 时,
时,
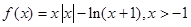
当
 时,
时,
 ,
,
 ,
,
 在
在
 上是减函数;
上是减函数;
当
 时,
时,
 ,
,
 ,令
,令
 得,
得,
 ,
,
 在
在
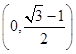 上单减,在
上单减,在
 上单增
上单增
综上得,
 的单减区间是
的单减区间是
 ,单增区间是
,单增区间是
 . 4分
. 4分
(2)当
 时,
时,

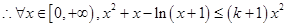
即
 ,设
,设
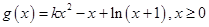 5分
5分
当
 时,
时,
 ,不合题意; 6分
,不合题意; 6分
当
 时,
时,

令
 得,
得,
 ,
,

 时,
时,
 ,
,
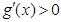 在
在
 上恒成立,
上恒成立,
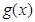 在
在
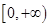 上单增,
上单增,
 ,故
,故
 符合题意; 8分
符合题意; 8分
②当
 时,
时,
 ,对
,对
 ,
,
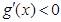 ,
,
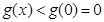 ,
,
故
 不合题意.综上,
不合题意.综上,
 的最小值为
的最小值为
 . 9分
. 9分
(3)由(2)得,
 ①
①
证明:当n=1时,不等式左边=2-ln3<2=右边,所以不等式成立.
当n≥2时,令①式中
 得
得
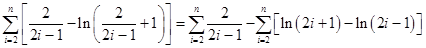

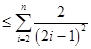
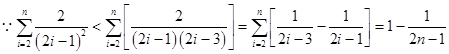 ,
,
 ,
,
 ,
,
所以当n≥2时不等式成立.
命题得证. 14分
【简答题】

[5/2000]已知a≤ 【图片】+ln x对任意x∈[ 【图片】,2]恒成立,则a的最大值为( ) A.0B.1C.2D.3
参考答案:
|
A
|
参考解析:
设f(x)=
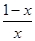 +ln x,则f′(x)=
+ln x,则f′(x)=
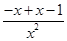 +
+
 =
=
 .当x∈[
.当x∈[
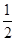 ,1)时,f′(x)<0,故函数f(x)在[
,1)时,f′(x)<0,故函数f(x)在[
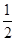 ,1)上单调递减;当x∈(1,2]时,f′(x)>0,故函数f(x)在(1,2]上单调递增,∴f(x)
min=f(1)=0,∴a≤0,即a的最大值为0.
,1)上单调递减;当x∈(1,2]时,f′(x)>0,故函数f(x)在(1,2]上单调递增,∴f(x)
min=f(1)=0,∴a≤0,即a的最大值为0.
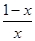 +ln x,则f′(x)=
+ln x,则f′(x)=
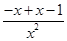 +
+
 =
=
 .当x∈[
.当x∈[
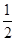 ,1)时,f′(x)<0,故函数f(x)在[
,1)时,f′(x)<0,故函数f(x)在[
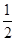 ,1)上单调递减;当x∈(1,2]时,f′(x)>0,故函数f(x)在(1,2]上单调递增,∴f(x)
min=f(1)=0,∴a≤0,即a的最大值为0.
,1)上单调递减;当x∈(1,2]时,f′(x)>0,故函数f(x)在(1,2]上单调递增,∴f(x)
min=f(1)=0,∴a≤0,即a的最大值为0.
【简答题】

[6/2000]已知a为实数f(x)=(x2-4)(x-a),(1)求导函数f′(x);(2)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;(3)若...
参考答案:
| 解:(1)由原式得f(x)=x3-ax2-4x+4a, ∴f′(x)=3x2-2ax-4; (2)由f′(-1)=0得  ,此时有f(x)=(x2-4) ,此时有f(x)=(x2-4) ,f′(x)=3x2-x-4, ,f′(x)=3x2-x-4,由f′(x)=0得  或x=-1, 或x=-1,又 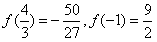 ,f(-2)=0,f(2)=0, ,f(-2)=0,f(2)=0,所以f(x)在[-2,2]上的最大值为  ,最小值为 ,最小值为 。 。(3)f′(x)=3x2-2ax-4的图象为开口向上且过点(0,-4)的抛物线, 由条件得f′(-2)≥0,f′(2)≥0,即 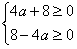 , ,∴-2≤a≤2, 所以a的取值范围为[-2,2]。 |
参考解析:
无
【简答题】

[7/2000]函数y=x+ 1x在x=1处的导数是______.
参考答案:
由y=x+
所以,y′|x=1=1-1=0. 故答案为0. |
参考解析:
无
【简答题】

[8/2000]下面四图都是在同一坐标系中某三次函数及其导函数的图像,其中一定不正确的序号是( ) 【图片】A.①②B.③④C.①③D.①④
参考答案:
|
B
|
参考解析:
解:由图象可知,在图①、②在每个区间上函数的单调性与对应的导数的符号是正确的,即单调增区间导数大于零,单调减区间上导数小于零;在③中显示在区间
 上导函数的值为负值,而该区间上的函数图象显示不单调,二者不一致,所以③不正确;在④图象显示在区间
上导函数的值为负值,而该区间上的函数图象显示不单调,二者不一致,所以③不正确;在④图象显示在区间
 上导函数的值总为正数,而相应区间上的函数图象却显示为减函数,二者相矛盾,所以不正确.故选B.
上导函数的值总为正数,而相应区间上的函数图象却显示为减函数,二者相矛盾,所以不正确.故选B.

【简答题】

[9/2000]已知函数 【图片】. (Ⅰ)求函数 【图片】的单调区间; (Ⅱ)若函数 【图片】在区间 【图片】上是减函数,求实数 【图片】的最小值; (Ⅲ)若存在 ...
参考答案:
|
(Ⅰ)函数
 的减区间是 的减区间是
 ,增区间是 ,增区间是
 ; ;
(Ⅱ)  的最小值为 的最小值为
 ;(Ⅲ) ;(Ⅲ)
 . .
|
参考解析:
(Ⅰ)求出
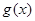 的导数
的导数
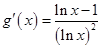 ,由
,由
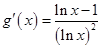 的符号确定
的符号确定
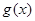 的单调区间;
的单调区间;
(Ⅱ)求出
 的导数
的导数
 ,由
,由
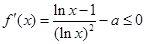 在
在
 上恒成立求得实数
上恒成立求得实数
 的最小值;(Ⅲ)注意左右两边的自变量
的最小值;(Ⅲ)注意左右两边的自变量
 是独立的.若存在
是独立的.若存在
 使
使
 成立,则
成立,则
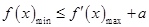 .故首先求出
.故首先求出
 然后解不等式求实数
然后解不等式求实数
 的取值范围.
的取值范围.
解:(Ⅰ)由
 得,
得,
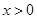 且
且
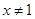 ,则函数
,则函数
 的定义域为
的定义域为
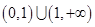 ,
,
且
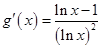 ,令
,令
 ,即
,即
 ,解得
,解得
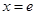
当
 且
且
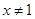 时,
时,
 ;当
;当
 时
时
 ,
,
 函数
函数
 的减区间是
的减区间是
 ,增区间是
,增区间是
 4分
4分
(Ⅱ)由题意得:函数
 在
在
 上是减函数,
上是减函数,
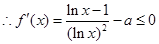 在
在
 上恒成立,即
上恒成立,即
 在
在
 上恒成立
上恒成立
令
 ,因此
,因此
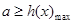 即可
即可

当且仅当
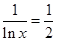 ,即
,即
 时取等号
时取等号
 因此
因此
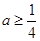 ,故
,故
 的最小值为
的最小值为
 . 8分
. 8分
(Ⅲ)命题“若存在
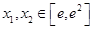 ,使
,使
 ,”等价于
,”等价于
“当
 时,有
时,有
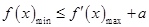 ”,
”,
由(Ⅱ)得,当
 时,
时,
 ,则
,则
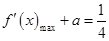 ,
,
故问题等价于:“当
 时,有
时,有
 ”,
”,
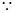
 ,由(Ⅱ)知
,由(Ⅱ)知
 ,
,
(1)当
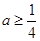 时,
时,
 在
在
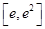 上恒成立,因此
上恒成立,因此
 在
在
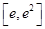 上为减函数,则
上为减函数,则
 ,故
,故
 ,
,
(2)当
 时,
时,
 在
在
 上恒成立,因此
上恒成立,因此
 在
在
 上为增函数,
上为增函数,
则
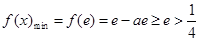 ,不合题意
,不合题意
(3)当
 时,由于
时,由于
 在
在
 上为增函数,
上为增函数,
故
 的值域为
的值域为
 ,即
,即
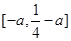
由
 的单调性和值域知,存在唯一
的单调性和值域知,存在唯一
 ,使
,使
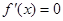 ,且满足:当
,且满足:当
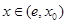 时,
时,
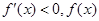 为减函数;当
为减函数;当
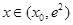 时,
时,
 为增函数;
为增函数;
所以,

所以,
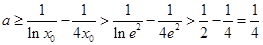 与
与
 矛盾,不合题意
矛盾,不合题意
综上,得
 . 12分
. 12分
【简答题】

[10/2000]设函数f(x)=lnx-ax,g(x)=e x-ax,其中a为实数. (1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值...
参考答案:
|
(1) a∈(e,+∞).
(2) 当a≤0或a=e -1时,f(x)的零点个数为1,当0<a<e -1时,f(x)的零点个数为2. 证明见解析 |
参考解析:
解:(1)令f′(x)=
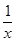 -a=
-a=
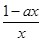 <0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a
-1,即f(x)在(a
-1,+∞)上是单调减函数.同理,f(x)在(0,a
-1)上是单调增函数.由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)⊆(a
-1,+∞),从而a
-1≤1,即a≥1.令g′(x)=e
x-a=0,得x=ln a.当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.又g(x)在(1,+∞)上有最小值,所以ln a>1,即a>e.
<0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a
-1,即f(x)在(a
-1,+∞)上是单调减函数.同理,f(x)在(0,a
-1)上是单调增函数.由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)⊆(a
-1,+∞),从而a
-1≤1,即a≥1.令g′(x)=e
x-a=0,得x=ln a.当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.又g(x)在(1,+∞)上有最小值,所以ln a>1,即a>e.
综上,有a∈(e,+∞).
(2)当a≤0时,g(x)必为单调增函数;当a>0时,令g′(x)=e x-a>0,
解得a<e x,即x>ln a,因为g(x)在(-1,+∞)上是单调增函数,类似(1)有ln a≤-1,即0<a≤e -1.结合上述两种情况,有a≤e -1.
(ⅰ)当a=0时,由f(1)=0以及f′(x)=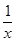 >0,得f(x)存在唯一的零点;
>0,得f(x)存在唯一的零点;
(ⅱ)当a<0时,由于f(e a)=a-ae a=a(1-e a)<0,f(1)=-a>0,且函数f(x)在[e a,1]上的图象不间断,所以f(x)在(e a,1)上存在零点.另外,当x>0时,f′(x)=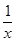 -a>0,故f(x)在(0,+∞)上是单调增函数,所以f(x)只有一个零点.
-a>0,故f(x)在(0,+∞)上是单调增函数,所以f(x)只有一个零点.
(ⅲ)当0<a≤e -1时,令f′(x)=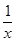 -a=0,解得x=a
-1.当0<x<a
-1时,f′(x)>0,当x>a
-1时,f′(x)<0,所以,x=a
-1是f(x)的最大值点,且最大值为f(a
-1)=-ln a-1.
-a=0,解得x=a
-1.当0<x<a
-1时,f′(x)>0,当x>a
-1时,f′(x)<0,所以,x=a
-1是f(x)的最大值点,且最大值为f(a
-1)=-ln a-1.
①当-ln a-1=0,即a=e -1时,f(x)有一个零点x=e.
②当-ln a-1>0,即0<a<e -1时,f(x)有两个零点.
实际上,对于0<a<e -1,由于f(e -1)=-1-ae -1<0,f(a -1)>0,且函数f(x)在[e -1,a -1]上的图象不间断,所以f(x)在(e -1,a -1)上存在零点.
另外,当x∈(0,a -1)时,f′(x)=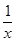 -a>0,故f(x)在(0,a
-1)上是单调增函数,所以f(x)在(0,a
-1)上只有一个零点.
-a>0,故f(x)在(0,a
-1)上是单调增函数,所以f(x)在(0,a
-1)上只有一个零点.
下面考虑f(x)在(a -1,+∞)上的情况.先证f(e a -1)=a(a -2-e a -1)<0.
为此,我们要证明:当x>e时,e x>x 2.设h(x)=e x-x 2,则h′(x)=e x-2x,再设l(x)=h′(x)=e x-2x,则l′(x)=e x-2.
当x>1时,l′(x)=e x-2>e-2>0,所以l(x)=h′(x)在(1,+∞)上是单调增函数.故当x>2时,h′(x)=e x-2x>h′(2)=e 2-4>0,从而h(x)在(2,+∞)上是单调增函数.进而当x>e时,
h(x)=e x-x 2>h(e)=e e-e2>0.即当x>e时,e x>x 2.
当0<a<e -1,即a -1>e时,f(e a -1)=a -1-ae a -1=a(a -2-e a -1)<0,又f(a -1)>0,且函数f(x)在[a -1,e a -1]上的图象不间断,所以f(x)在(a -1,e a -1)上存在零点.又当x>a -1时,f′(x)=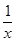 -a<0,故f(x)在(a
-1,+∞)上是单调减函数,所以f(x)在(a
-1,+∞)上只有一个零点.
-a<0,故f(x)在(a
-1,+∞)上是单调减函数,所以f(x)在(a
-1,+∞)上只有一个零点.
综合(ⅰ),(ⅱ),(ⅲ),当a≤0或a=e -1时,f(x)的零点个数为1,当0<a<e -1时,f(x)的零点个数为2.
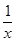 -a=
-a=
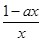 <0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a
-1,即f(x)在(a
-1,+∞)上是单调减函数.同理,f(x)在(0,a
-1)上是单调增函数.由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)⊆(a
-1,+∞),从而a
-1≤1,即a≥1.令g′(x)=e
x-a=0,得x=ln a.当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.又g(x)在(1,+∞)上有最小值,所以ln a>1,即a>e.
<0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a
-1,即f(x)在(a
-1,+∞)上是单调减函数.同理,f(x)在(0,a
-1)上是单调增函数.由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)⊆(a
-1,+∞),从而a
-1≤1,即a≥1.令g′(x)=e
x-a=0,得x=ln a.当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.又g(x)在(1,+∞)上有最小值,所以ln a>1,即a>e.
综上,有a∈(e,+∞).
(2)当a≤0时,g(x)必为单调增函数;当a>0时,令g′(x)=e x-a>0,
解得a<e x,即x>ln a,因为g(x)在(-1,+∞)上是单调增函数,类似(1)有ln a≤-1,即0<a≤e -1.结合上述两种情况,有a≤e -1.
(ⅰ)当a=0时,由f(1)=0以及f′(x)=
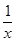 >0,得f(x)存在唯一的零点;
>0,得f(x)存在唯一的零点;
(ⅱ)当a<0时,由于f(e a)=a-ae a=a(1-e a)<0,f(1)=-a>0,且函数f(x)在[e a,1]上的图象不间断,所以f(x)在(e a,1)上存在零点.另外,当x>0时,f′(x)=
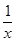 -a>0,故f(x)在(0,+∞)上是单调增函数,所以f(x)只有一个零点.
-a>0,故f(x)在(0,+∞)上是单调增函数,所以f(x)只有一个零点.
(ⅲ)当0<a≤e -1时,令f′(x)=
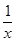 -a=0,解得x=a
-1.当0<x<a
-1时,f′(x)>0,当x>a
-1时,f′(x)<0,所以,x=a
-1是f(x)的最大值点,且最大值为f(a
-1)=-ln a-1.
-a=0,解得x=a
-1.当0<x<a
-1时,f′(x)>0,当x>a
-1时,f′(x)<0,所以,x=a
-1是f(x)的最大值点,且最大值为f(a
-1)=-ln a-1.
①当-ln a-1=0,即a=e -1时,f(x)有一个零点x=e.
②当-ln a-1>0,即0<a<e -1时,f(x)有两个零点.
实际上,对于0<a<e -1,由于f(e -1)=-1-ae -1<0,f(a -1)>0,且函数f(x)在[e -1,a -1]上的图象不间断,所以f(x)在(e -1,a -1)上存在零点.
另外,当x∈(0,a -1)时,f′(x)=
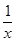 -a>0,故f(x)在(0,a
-1)上是单调增函数,所以f(x)在(0,a
-1)上只有一个零点.
-a>0,故f(x)在(0,a
-1)上是单调增函数,所以f(x)在(0,a
-1)上只有一个零点.
下面考虑f(x)在(a -1,+∞)上的情况.先证f(e a -1)=a(a -2-e a -1)<0.
为此,我们要证明:当x>e时,e x>x 2.设h(x)=e x-x 2,则h′(x)=e x-2x,再设l(x)=h′(x)=e x-2x,则l′(x)=e x-2.
当x>1时,l′(x)=e x-2>e-2>0,所以l(x)=h′(x)在(1,+∞)上是单调增函数.故当x>2时,h′(x)=e x-2x>h′(2)=e 2-4>0,从而h(x)在(2,+∞)上是单调增函数.进而当x>e时,
h(x)=e x-x 2>h(e)=e e-e2>0.即当x>e时,e x>x 2.
当0<a<e -1,即a -1>e时,f(e a -1)=a -1-ae a -1=a(a -2-e a -1)<0,又f(a -1)>0,且函数f(x)在[a -1,e a -1]上的图象不间断,所以f(x)在(a -1,e a -1)上存在零点.又当x>a -1时,f′(x)=
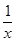 -a<0,故f(x)在(a
-1,+∞)上是单调减函数,所以f(x)在(a
-1,+∞)上只有一个零点.
-a<0,故f(x)在(a
-1,+∞)上是单调减函数,所以f(x)在(a
-1,+∞)上只有一个零点.
综合(ⅰ),(ⅱ),(ⅲ),当a≤0或a=e -1时,f(x)的零点个数为1,当0<a<e -1时,f(x)的零点个数为2.